A - Mục đích, yêu cầu
- HS bước đầu biết được các đối tượng hình học cơ bản của phần mềm và quan hệ giữa chúng.
- HS biết và thao tác được một số lệnh đơn giản liên quan đến điểm, đoạn, đường thẳng và cách thiết lập quan hệ giữa chúng.
- Thông qua phần mềm HS biết được các ứng dụng của phần mềm trong việc vẽ và minh hoạ các hình hình học được học trong chương trình môn Toán.
B - Những điểm cần lưu ý và gợi ý dạy học
a) GeoGebra là một phần mềm vẽ hình hình học động tương đối đơn giản nhưng hay và rất phù hợp với môn Toán (hình học phẳng) trong trường phổ thông.
b) Phần mềm này dự kiến được đưa vào chương trình môn Tin học dành cho cả các lớp 6, 7, 8 do vậy GV cần chủ động nghiên cứu tìm hiểu các chức năng khác của phần mềm để chuẩn bị giảng dạy cho các năm tiếp theo.
c) Phần kiến thức quan trọng nhất cần trình bày cho HS là khái niệm quan hệ giữa các đối tượng toán học. Chính các quan hệ lôgic chặt chẽ giữa các đối tượng hình học sẽ tạo ra khái niệm “hình học động” của phần mềm. Và đây là điểm khác biệt nhất của phần mềm này với các phần mềm đồ hoạ khác.
d) Quan hệ toán học đầu tiên cần hướng dẫn cho HS là quan hệ giữa các số, biểu thức và hàm số.
Ví dụ các số, hàm số tự do:
m := 1
f(x) := 2x - 1
Các số và hàm sau đây sẽ là phụ thuộc:
a := 2(m - 1)
g(x) := m*x + f(x)
e) Các quan hệ hình học chính cần dạy trong bài học này là:
- Quan hệ thuộc;
- Giao điểm;
- Trung điểm;
- Đường song song;
- Đường vuông góc;
- Đường phân giác.
Mỗi quan hệ được xác định bởi một công cụ. Sử dụng thành thạo các công cụ này là nội dung chủ yếu của bài học cần dạy cho HS.
f) Màn hình làm việc của GeoGebra có nhiều vùng làm việc khác nhau. Các khu vực làm việc có thể cần xuất hiện bao gồm:
- Lưới ô vuông trên mặt phẳng;
- Các trục toạ độ vuông góc;
- Cửa sổ “đại số” phía trái là nơi hiện thông tin các đối tượng hình học;
Dòng lệnh phía dưới màn hình cho phép nhập trực tiếp các đối tượng hình học thông qua việc gõ lệnh.
- Cửa sổ CAS dùng để thực hiện các lệnh tính toán số học, đại số chính xác.
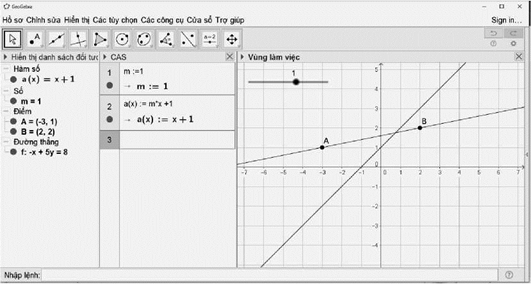
Các vùng làm việc trên đều có thể ẩn đi bằng các lệnh từ bảng chọn View. Trong chương trình của sách này, GV và HS chủ yếu dùng các lệnh từ thanh công cụ của phần mềm.
g) Một trong những kiến thức trọng tâm của bài học này là quan hệ phụ thuộc toán học giữa các đối tượng trong GeoGebra. HS cần biết những điều này. Chú ý rằng quan hệ này rất đa dạng. Xét bảng các ví dụ sau:
Quan hệ |
Đối
tượng
cha |
Đối tượng con |
Nhận xét |
| Điểm A nằm trên đường thẳng d. |
d |
A |
1 cha,1 con |
| A là giao của hai đường d1, d2. |
d1, d2 |
A |
2 cha,1 con |
| 2 đường tròn c1, c2 giao nhau tại 2 điểm A, B |
C1,C2 |
A, B |
2 cha, 2 con |
3 điểm A, B, C nằm trên đường tròn
P |
p |
A, B, C |
1 cha,3 con |
| Đường tròn p đi qua 3 điểm A, B, C. |
A, B, C |
p |
3 cha,1 con |
Quan hệ phụ thuộc toán học không chỉ ở một mức cha-con, mà còn nhiều mức.
h) Bài học dự kiến được giảng dạy trong 4 tiết, trong đó có 2 tiết lí thuyết và 2 tiết thực hành trên máy tính. Dự kiến lịch trình giảng dạy như sau:
Tiết 1: Khởi động phần mềm, vào/ra tệp. Khái niệm quan hệ toán học trong phần mềm. Các đối tượng đại số ban đầu: số, hàm số. Các đối tượng hình học ban đầu: điểm, đoạn thẳng, đường thẳng.
Tiết 2: Quan hệ giữa các đối tượng: quan hệ thuộc, giao điểm, trung điểm, vuông góc. Cách thiết lập các quan hệ này.
Tiết 3: Các công cụ vẽ góc. Quan hệ song song, đường phân giác.
Tiết 4: Các chức năng liên quan đến điều khiển và thể hiện các đối tượng hình học trên màn hình. Làm việc với nhãn và các tính chất khác của các đối tượng hình học.
i) Danh sách các công cụ hình học phẳng của GeoGebra.
Bảng sau cho biết các công cụ của phần mềm GeoGebra. GV cần chủ động xem trước để hiểu và chuẩn bị giảng dạy phần mềm này cho năm học tiếp theo.
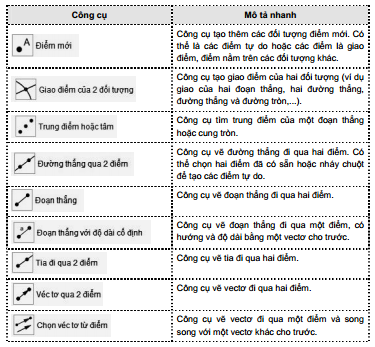

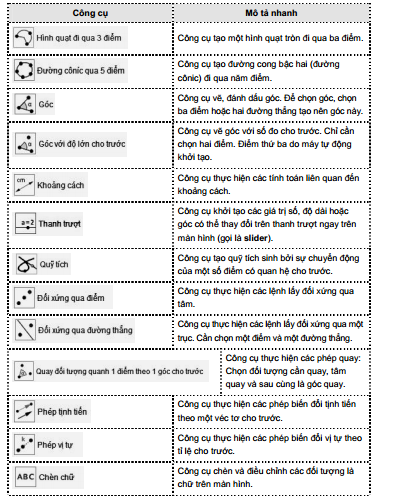
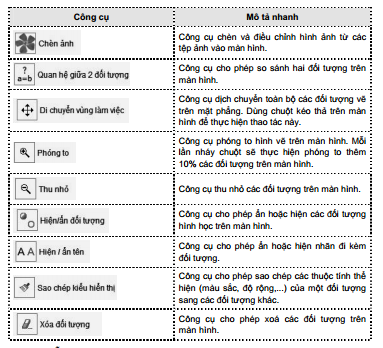
Hướng dẫn trả lời câu hỏi và bài tập
1. Gợi ý vẽ:
- Dùng công cụ đoạn thẳng hoặc đa giác để vẽ tam giác ABC.
- Dùng công cụ trung điểm để tạo ba trung điểm của ba cạnh tam giác.
- Dùng công cụ đoạn thẳng để vẽ ba đường trung tuyến.
- Dùng công cụ điểm để tạo điểm giao G của các đường trung tuyến này.
2. Gợi ý vẽ:
- Dùng công cụ đoạn thẳng hoặc đa giác để vẽ tam giác ABC.
- Dùng công cụ đường vuông góc để vẽ ba đường cao, hạ từ các đỉnh và vuông góc với các cạnh đối diện.
- Dùng công cụ điểm để tạo điểm giao H của các đường cao này.
3. Gợi ý vẽ:
- Dùng công cụ đoạn thẳng hoặc đa giác để vẽ tam giác ABC.
- Dùng công cụ đường phân giác để vẽ ba đường phân giác của các góc trong tam giác ABC.
- Dùng công cụ điểm để tạo điểm giao I của các đường phân giác này.
4. Có thể vẽ như sau:
- Dùng công cụ điểm tạo ba điểm bất kì, đặt tên các điểm này là A, B, C.
- Dùng công cụ song song kẻ từ A đường thẳng song song với BC, kẻ từ C đường thẳng song song với AB.
- Dùng công cụ điểm tạo điểm giao của hai đường song song trên, đặt tên điểm là D.
- Làm ẩn đi hai đường thẳng song song.
- Dùng công cụ đoạn thẳng nối và tạo hai đoạn thẳng AD, CD.
5. Gợi ý vẽ:
- Dùng công cụ đoạn thẳng hoặc đa giác để vẽ tam giác ABC.
- Dùng công cụ trung trực để tạo ra ba đường thẳng là trung trực của các cạnh AB, BC, CA.
- Dùng công cụ điểm để tạo giao điểm O của các đường trung trực này.
7. Cách vẽ gần giống như bài 2, nhưng có khác biệt. Gợi ý cách vẽ:
- Dùng công cụ điểm tạo ra ba điểm bất kì A, B, C trên mặt phẳng.
- Dùng công cụ đường thẳng (chú ý không phải công cụ đoạn thẳng), vẽ các đường thẳng AB, BC, CA.
- Dùng công cụ đường vuông góc để vẽ ba đường cao, hạ từ các đỉnh và vuông góc với các đường thẳng nối các cạnh đối diện.
- Dùng công cụ điểm để tạo điểm giao H của các đường cao tuyến này.
- Thay đổi kiểu thể hiện của ba đường thẳng AB, BC, CA về dạng đường nét đứt.
- Dùng công cụ đoạn thẳng nối tạo ra các cạnh AB, BC, CA.