Đề kiểm tra 45 phút học kỳ I Toán 6, Chương I: Ôn tập và bổ túc về số tự nhiên (Đề 20)
Giải Sách
2020-05-10T09:25:35-04:00
2020-05-10T09:25:35-04:00
https://baihochay.com/toan-hoc-6/de-kiem-tra-45-phut-hoc-ky-i-toan-6-chuong-i-on-tap-va-bo-tuc-ve-so-tu-nhien-de-20-4915.html
https://baihochay.com/uploads/news/2020_04/de-kiem-tra-toan-6.jpg
Bài học hay
https://baihochay.com/uploads/bai-hoc-hay-logo.png
Chủ nhật - 10/05/2020 09:24
Đề kiểm tra 45 phút học kỳ I Toán 6, Chương I: Ôn tập và bổ túc về số tự nhiên, Có hướng dẫn giải
Bài 1. (2 điểm) Cho tổng M = 85 + 195 + 60 + a với a G N. Tìm điều kiện của a để M chia hết cho 5, để M không chia hết cho 5.
Bài 2. (2 điểm)
a) Điền vào dấu * để được số 792* chia hết cho cả 2 và 5.
b) Điền vào dấu * để được số 25*3 chia hết cho 3.
Bài 3. (3 điểm)
a) Tìm các số tự nhiên x sao cho x + 16 chia hết cho x + 1.
b) Tìm số tự nhiên y lớn nhất, biết rằng 600 : y, 480 : y, 360 : y.
Bài 4. (2 điểm) Tìm số tự nhiên a nhỏ nhất sao cho chia a cho 5, cho 7, cho 11 được dư lần lượt là 3 ; 4 ; 6.
Bài 5. (1 điểm) Có tồn tại hay không hai số tự nhiên a, b sao cho (a + b)(a - b) = 975602.
HƯỚNG DẪN GIẢI
Bài 1. Nếu a ⋮ 5 thì M ⋮ 5
Nếu a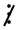 
5 thì M 
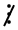5
Bài 2. a) * = 0
b) * ∈ {2 ; 5 ; 8}
Bài 3. a) x + 16 = (x + 1) + 15 : x = x + 1
Mà x + 1 ⋮ x + 1
Nên có 15 ⋮ x + 1
x + 1 ∈ {1 ; 3 ; 5 ; 15}
x ∈ {0 ; 2 ; 4 ; 14}
b) y = 120
Bài 4. Ta có a chia cho 5 ; 7 ; 11 dư lần lượt là 3 ; 4 ; 6 và a nhỏ nhất.
Do đó 2a chia cho 5 ; 7 ; 11 đều dư 1
Nên 2a - 1 là BCNN(5, 7, 11)
BCNN(5, 7, 11) = 5.7.11 = 385
Ta có 2a - 1 = 385
2a = 386
a = 193
Bài 5. Ta có (a + b) + (a - b) = a + b + a - b = 2a là số chẵn.
Do đó a + b, a - b cùng chẵn hoặc cùng lẻ
Suy ra (a + b)(a - b) là số chia hết cho 4 hoặc là số lẻ
Số 975602 là số chẵn và không chia hết cho 4
Vậy không tồn tại a, b ∈ N để có (a + b)(a - b) = 975602