Học tốt Toán 7, Phần hình học, chương II, Bài 4. Trường hợp bằng nhau thứ hai của tam giác CẠNH – GÓC – CẠNH (C.G.C)
Giải Sách
2019-08-29T12:00:25-04:00
2019-08-29T12:00:25-04:00
https://baihochay.com/index.php/toan-hoc-7/hoc-tot-toan-7-phan-hinh-hoc-chuong-ii-bai-4-truong-hop-bang-nhau-thu-hai-cua-tam-giac-canh-goc-canh-c-g-c-3765.html
/themes/linebox/images/no_image.gif
Bài học hay
https://baihochay.com/uploads/bai-hoc-hay-logo.png
Thứ năm - 29/08/2019 11:57
Hệ thống kiến thức lí thuyết cần nhớ, hướng dẫn giải bài tập SGK Toán 7, Bài 4. Trường hợp bằng nhau thứ hai của tam giác CẠNH – GÓC – CẠNH (C.G.C)
A.Tóm tắt kiến thức1. Trường hợp bằng nhau: cạnh - góc - cạnh (c.g.c)Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
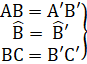 => ∆ ABC = ∆ A'B'C'(c.g.c) .2. Hệ quả. Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.B. Ví dụ giải toánVí dụ. Cho ∆ ABC, gọi M. N là trung điểm của AB. AC. Trên tia đối của tia MC lấy điểm K sao cho MK = MC.a) Chứng minh ∆ AMK = ∆ BMC.b) Trên tia đối của tịa NB lấy điểm I sao cho NI = NB. Chứng minh AI = BC.c) Chứng minh A là trung điểm của IK.Giải. a) Xét ∆ AMK và ∆ BMC có:AM = MB (giả thiết),MC = MK (giả thiết),
=> ∆ ABC = ∆ A'B'C'(c.g.c) .2. Hệ quả. Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.B. Ví dụ giải toánVí dụ. Cho ∆ ABC, gọi M. N là trung điểm của AB. AC. Trên tia đối của tia MC lấy điểm K sao cho MK = MC.a) Chứng minh ∆ AMK = ∆ BMC.b) Trên tia đối của tịa NB lấy điểm I sao cho NI = NB. Chứng minh AI = BC.c) Chứng minh A là trung điểm của IK.Giải. a) Xét ∆ AMK và ∆ BMC có:AM = MB (giả thiết),MC = MK (giả thiết),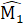 =
= 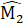 (đối đỉnh),do đó ∆ AMK = ∆ BMC (c.g.c).
(đối đỉnh),do đó ∆ AMK = ∆ BMC (c.g.c).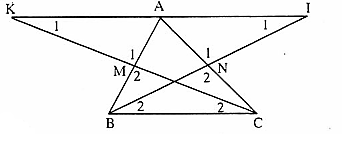 b) Xét ∆ ANI và ∆ CNB có:AN - CN (giả thiết),
b) Xét ∆ ANI và ∆ CNB có:AN - CN (giả thiết), 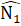 =
= 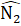 (đối đinh), NI = NB (giả thiết)do đó ∆ ANI = ∆ CNB(c.g.c). Suy ra AI = BC.∆ AMK = ∆ BMC (chứng minh trên) nên
(đối đinh), NI = NB (giả thiết)do đó ∆ ANI = ∆ CNB(c.g.c). Suy ra AI = BC.∆ AMK = ∆ BMC (chứng minh trên) nên 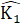 -
- 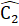 , AK = BC.Hai góc
, AK = BC.Hai góc 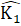 và
và 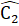 ở vị trí so le trong nên AK//BC. (1)∆ ANI = ∆ CNB (chứng minh trên) nên
ở vị trí so le trong nên AK//BC. (1)∆ ANI = ∆ CNB (chứng minh trên) nên 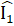 =
= 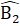 , , mà hai góc ở vị trí so le trong nên AI // BC. (2)Tir (1) và (2) suy ra I, A, K thẳng hàng (tiên đề Ơ-clít).Mặt khác AK = AI (= BC) nên A là trung điểm của IK.Nhận xét. Sai lầm dễ mắc của một số bạn trong bài trên là mới chứng minh được AI = AK đã vội kết luận A là trung điểm của IK.C. Hướng dẫn giải bài tập trong sách giáo khoaBài 24. (Bạn đọc tự vẽ hình) - Vẽ góc
, , mà hai góc ở vị trí so le trong nên AI // BC. (2)Tir (1) và (2) suy ra I, A, K thẳng hàng (tiên đề Ơ-clít).Mặt khác AK = AI (= BC) nên A là trung điểm của IK.Nhận xét. Sai lầm dễ mắc của một số bạn trong bài trên là mới chứng minh được AI = AK đã vội kết luận A là trung điểm của IK.C. Hướng dẫn giải bài tập trong sách giáo khoaBài 24. (Bạn đọc tự vẽ hình) - Vẽ góc 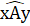 = 90°.-Trên tia Ax vẽ đoạn thẳng AB = 3cm.-Trên tia Ay vẽ đoạn thẳng AC = 3cm.-Vẽ đoạn thẳng BC.-Dùng thước đo góc, ta đo được
= 90°.-Trên tia Ax vẽ đoạn thẳng AB = 3cm.-Trên tia Ay vẽ đoạn thẳng AC = 3cm.-Vẽ đoạn thẳng BC.-Dùng thước đo góc, ta đo được 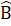 =
= 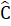 = 45° .Bài 25. Hình 82 (SGK). Xét ∆ ADB và ∆ ADE có:AB = AE (giả thiết), Â1 = Â2 , AD cạnh chung.Suy ra ∆ ADB = ∆ ADE (c.g.c).Hình 83 (SGK). ∆ HGK và ∆ IKG có:HG = IK (giả thiết),
= 45° .Bài 25. Hình 82 (SGK). Xét ∆ ADB và ∆ ADE có:AB = AE (giả thiết), Â1 = Â2 , AD cạnh chung.Suy ra ∆ ADB = ∆ ADE (c.g.c).Hình 83 (SGK). ∆ HGK và ∆ IKG có:HG = IK (giả thiết), 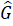 =
= 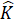 , GK cạnh chung (giả thiết).Suy ra ∆ HGK = ∆ IKG (c.g.c).Hình 84 (SGK). ∆ PMQ và ∆ PMN có: MP cạnh chung,
, GK cạnh chung (giả thiết).Suy ra ∆ HGK = ∆ IKG (c.g.c).Hình 84 (SGK). ∆ PMQ và ∆ PMN có: MP cạnh chung, 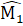 =
= 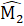 , nhưng MN không bằng MQ nên ∆ PMQ không bằng ∆ PMN.Nhận xét. Khi xét hai tam giác bằng nhau theo trường hợp c.g.c hay không, chúng ta phải chú ý yếu tố góc xen giữa.Bài 26. Thứ tự sắp xếp là: 5), 1), 2), 4), 3).∆ AMBvà ∆ EMC có:MB = MC (giả thiết),
, nhưng MN không bằng MQ nên ∆ PMQ không bằng ∆ PMN.Nhận xét. Khi xét hai tam giác bằng nhau theo trường hợp c.g.c hay không, chúng ta phải chú ý yếu tố góc xen giữa.Bài 26. Thứ tự sắp xếp là: 5), 1), 2), 4), 3).∆ AMBvà ∆ EMC có:MB = MC (giả thiết),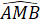 =
= 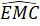 (hai góc đối đỉnh),MA = ME (giả thiết).Do đó ∆ AMB= ∆ EMC(c.g.c).∆ AMB = ∆ EMC =>
(hai góc đối đỉnh),MA = ME (giả thiết).Do đó ∆ AMB= ∆ EMC(c.g.c).∆ AMB = ∆ EMC => 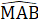 =
= 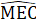 (hai góc tương ứng).
(hai góc tương ứng).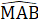 =
= 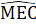 => AB // CE (có hai góc so le trong bằng nhau).Bài 27. Hình 86 (SGK). Thêm
=> AB // CE (có hai góc so le trong bằng nhau).Bài 27. Hình 86 (SGK). Thêm 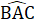 =
= 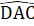 thì ∆ ABC = ∆ ADC(c.g.c).Hình 87 (SGK). Thêm MA = ME thì ∆ AMB = ∆ EMC(c.g.c).Hình 88 (SGK). Thêm AC = BD thì ∆ CAB = ∆ DBA (c.g.c).Bài 28. Ta tính được
thì ∆ ABC = ∆ ADC(c.g.c).Hình 87 (SGK). Thêm MA = ME thì ∆ AMB = ∆ EMC(c.g.c).Hình 88 (SGK). Thêm AC = BD thì ∆ CAB = ∆ DBA (c.g.c).Bài 28. Ta tính được 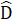 = 180° - 80° - 40° = 60°. ∆ ABC và ∆ KDE có:AB = KD (giả thiết),
= 180° - 80° - 40° = 60°. ∆ ABC và ∆ KDE có:AB = KD (giả thiết), 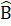 =
= 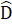 (=60°), BC = DE (giả thiết).Do đó ∆ ABC - ∆ KDE(c.g.c).Chú ý- ∆ ABC và ∆ MNP có AB = MN, BC = NP nhưng đề bài không cho B
(=60°), BC = DE (giả thiết).Do đó ∆ ABC - ∆ KDE(c.g.c).Chú ý- ∆ ABC và ∆ MNP có AB = MN, BC = NP nhưng đề bài không cho B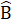 =
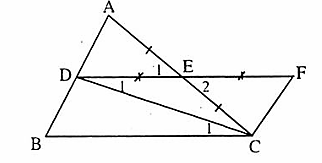
=  nên ta không kết luận được ∆ ABC = ∆ MNP.- ∆ ABCvà ∆ NMPcó AB = NM, B = M nhưng đề bài không cho BC = MP nên ta không kết luận được ∆ ABC = ∆ NMP.Bài 29. Ta có AC = AD + DC, AE = AB + BE mà AD = AB, DC = BEnên AC = AE.∆ ABC và ∆ ADE có:AC = AE (chứng minh trên), chung,AB = AD (giả thiết).Vậy ∆ ABC= ∆ ADE (c.g.c).
nên ta không kết luận được ∆ ABC = ∆ MNP.- ∆ ABCvà ∆ NMPcó AB = NM, B = M nhưng đề bài không cho BC = MP nên ta không kết luận được ∆ ABC = ∆ NMP.Bài 29. Ta có AC = AD + DC, AE = AB + BE mà AD = AB, DC = BEnên AC = AE.∆ ABC và ∆ ADE có:AC = AE (chứng minh trên), chung,AB = AD (giả thiết).Vậy ∆ ABC= ∆ ADE (c.g.c).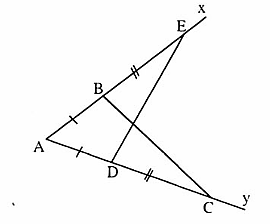 Bài 30. Góc ABC không phải là góc xen giữa hai cạnh BC và CA, góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh - góc - cạnh để kết luận ∆ ABC = ∆ A'BC được.Bài 31. ∆ MHA và ∆ MHB có:MH: cạnh chung;
Bài 30. Góc ABC không phải là góc xen giữa hai cạnh BC và CA, góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh - góc - cạnh để kết luận ∆ ABC = ∆ A'BC được.Bài 31. ∆ MHA và ∆ MHB có:MH: cạnh chung;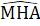 =
= 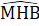 = 90° (định nghĩa đường trung trực); HA = HB (định nghĩa đường trung trực).Do đó ∆ MHA = ∆ MHB (c.g.c) suy ra MA = MB (hai cạnh tương ứng).
= 90° (định nghĩa đường trung trực); HA = HB (định nghĩa đường trung trực).Do đó ∆ MHA = ∆ MHB (c.g.c) suy ra MA = MB (hai cạnh tương ứng).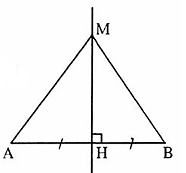 Bài 32. ∆ AHB = ∆ KHB(c.g.c) =>
Bài 32. ∆ AHB = ∆ KHB(c.g.c) => 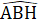 =
= 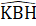 => BH là tia phân giác của góc B.∆ AHC = ∆ KHC(c.g.c) =>
=> BH là tia phân giác của góc B.∆ AHC = ∆ KHC(c.g.c) => 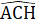 =
= 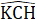
=>CH là tia phân giác của góc C.Ngoài ra còn có: HA và HK là các tia phàn giác của góc bẹt BHC; HB và HC là các tia phân giác của góc bẹt AHK.D. Bài tập luyện thêm1. Cho ∆ ABC = ∆ DEF. Gọi M, N lấn lượt là trung điểm của BC, EF. Chứng minh AM = DN.2. Cho góc xOy (khác góc bẹt). Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Tia phân giác Oz của góc xOy cắt AB tại C.a) Chứng minh ∆ AOC - ∆ BOC, từ đó suy ra OC ⊥ AB.b) Trên tia đối của tia co lấy điểm D sao cho CD = CO.Chứng minh AD = BO, AD // BO.c) Gọi M là trung điếm AD; N là trung điểm OB. Chứng minh M, c, N thẳng hàng.3. Cho ∆ ABC vuông tại A. Tia phân giác góc B cắt AC tại D.Trên BC lấy M sao cho BM = BA. Chứng minh DM ⊥ BC.4. Cho ∆ ABC nhọn. Kẻ BD ⊥ AC (D ∈ AC), CE ⊥ AB (E ∈ AB). Trên tia đối tia BD lấy điểm p sao cho BP = AC, trên tia đối của tia CE lấy điểm Q sao cho CQ = AB. Chứng minh AP = AQ, AP ⊥ AQ.5. Cho ∆ ABC. Gọi D, E theo thứ tự là trung điểm cúa AB, AC. Trên tia đối của tia ED lấy điểm F sao cho EF = ED. Chứng minh:a) BD = CF, AB // CF.b) ∆ BCD= ∆ FDC.c) DE // BC.6. Cho góc xOy khác góc bẹt. Trên cạnh Ox lấy điểm A và B (OA < OB). Trên cạnh Oy lấy điểm c và D sao cho OC = OA, OD = OB.Chứng minh:a) ∆ OAD = ∆ OCB.b) ∆ ACB= ∆ CAD.Lời giải - Hướng dẫn - Đáp số1. ∆ ABC = ∆ DEF nên AB = DE, 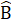 = Ê , BC = EF.Mặt khác BM = MC =
= Ê , BC = EF.Mặt khác BM = MC =  BC, EN = NF =
BC, EN = NF = 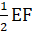 nên BM = EN.
nên BM = EN.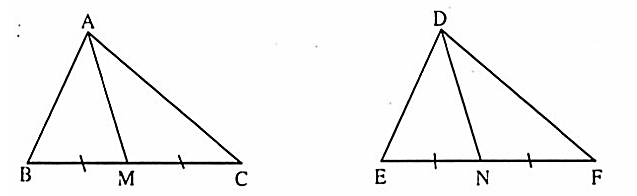 nên ∆ ABM = ∆ DEN (c.g.c). Suy ra AM = DN.Nhận xét. Đoạn thắng AM gọi là đường trung tuyến của ∆ABC. Như vậy hai tam giác bằng nhau thì hai đường trung tuyến tương ứng bằng nhau,2. a) Xét ∆ AOCvà ∆ BOCcó:OA = OB (giả thiết),
nên ∆ ABM = ∆ DEN (c.g.c). Suy ra AM = DN.Nhận xét. Đoạn thắng AM gọi là đường trung tuyến của ∆ABC. Như vậy hai tam giác bằng nhau thì hai đường trung tuyến tương ứng bằng nhau,2. a) Xét ∆ AOCvà ∆ BOCcó:OA = OB (giả thiết), 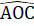 =
= 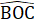 (giả thiết), OC cạnh chung.Do đó ∆ AOC = ∆ BOC (c.g.c), suy ra
(giả thiết), OC cạnh chung.Do đó ∆ AOC = ∆ BOC (c.g.c), suy ra 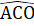 =
= 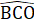 (góc tương ứng).Mặt khác
(góc tương ứng).Mặt khác 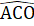 +
+ 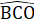 = 180° (kề bù).Suy ra
= 180° (kề bù).Suy ra 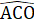 =
= 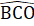 = 90° hay AB ⊥ OC.b) Xét ∆ ACD và ∆ BCO có:AC = BC (vì ∆ AOC = ∆ BOC);ACD = BCO. (đối đỉnh);CD = CO (giả thiết).Do đó ∆ ACD = ∆ BCO (c.g.c). Suy ra AD = OB,
= 90° hay AB ⊥ OC.b) Xét ∆ ACD và ∆ BCO có:AC = BC (vì ∆ AOC = ∆ BOC);ACD = BCO. (đối đỉnh);CD = CO (giả thiết).Do đó ∆ ACD = ∆ BCO (c.g.c). Suy ra AD = OB, 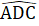 =
= 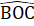 , mà hai góc ớ vị trí so le trong nên AD // BO.
, mà hai góc ớ vị trí so le trong nên AD // BO.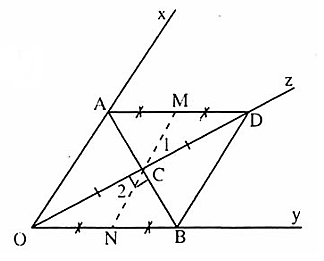 c) Xét ∆ MCD và ∆ NCOcó:MD = ON(vì
c) Xét ∆ MCD và ∆ NCOcó:MD = ON(vì  AD =
AD = 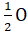 B);
B);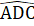 -
- 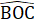 (chứng minh trên);OC = DC (giả thiết).Do đó ∆ DCM = ∆ OCN (c.g.c) suy ra
(chứng minh trên);OC = DC (giả thiết).Do đó ∆ DCM = ∆ OCN (c.g.c) suy ra 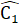 =
= 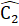 .Mặt khác
.Mặt khác 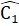 + = 180° nên C2
+ = 180° nên C2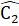 +
+ 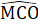 = 180° .Vậy M, C, N thẳng hàng.Nhận xét. Muốn chứng minh ba điểm thẳng hàng, ta chứng minh hai đoạn thẳng nối ba điểm đó tạo thành một góc có số đo bằng 180°.Xét ∆ ABD và ∆ MBDcó:BA = BM (giả thiết);
= 180° .Vậy M, C, N thẳng hàng.Nhận xét. Muốn chứng minh ba điểm thẳng hàng, ta chứng minh hai đoạn thẳng nối ba điểm đó tạo thành một góc có số đo bằng 180°.Xét ∆ ABD và ∆ MBDcó:BA = BM (giả thiết);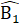 =
= 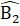 (giả thiết);BD là cạnh chung.Do đó ∆ ABD= ∆ MBD (c.g.c),suy ra
(giả thiết);BD là cạnh chung.Do đó ∆ ABD= ∆ MBD (c.g.c),suy ra 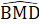 =
= 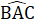 hay
hay 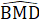 = 90° => DM ⊥ BC.Nhận xét. Để chứng minh một góc vuông, ta có thể chứng minh góc đó bằng một góc vuông sẵn có, bằng cách chứng minh hai tam giác bằng nhau.Từ các tam giác BDA, CEA vuông suy ra
= 90° => DM ⊥ BC.Nhận xét. Để chứng minh một góc vuông, ta có thể chứng minh góc đó bằng một góc vuông sẵn có, bằng cách chứng minh hai tam giác bằng nhau.Từ các tam giác BDA, CEA vuông suy ra 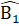 =
= 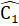 (cùng phụ với
(cùng phụ với 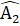 ).Mặt khác
).Mặt khác 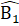 +
+ 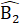 = 180° (kề bù),
= 180° (kề bù), 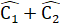 = 180° (kề bù)nên
= 180° (kề bù)nên 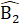 =
= 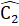 .Xét ∆ ABP và ∆ QCAcó:BP = AC (giả thiết);
.Xét ∆ ABP và ∆ QCAcó:BP = AC (giả thiết); 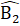 =
= 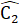 (chứng minh trên); AB = CQ (giả thiết).Do đó ∆ ABP= ∆ QCA (c.g.c).Suy ra AP = AQ; Q =
(chứng minh trên); AB = CQ (giả thiết).Do đó ∆ ABP= ∆ QCA (c.g.c).Suy ra AP = AQ; Q = 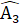 .=>
.=> 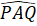 =
= 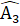 +
+ 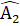 +
+ 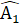 =
= 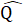 +
+ 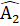 +
+ 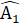 = 90°(vì ∆ AEQ vuông) hay AP ⊥ AQ.
= 90°(vì ∆ AEQ vuông) hay AP ⊥ AQ.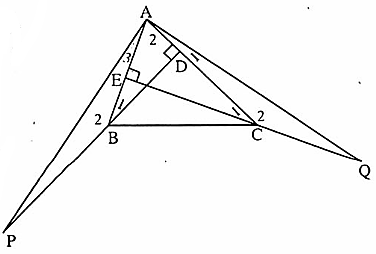 Nhận xét. Để chứng minh AP = AQ, ta thấy ∆ ABP và ∆ QCA có hai cặp cạnh bằng nhau nên ta tìm cách chứng tỏ cặp góc xen giữa bằng nhau.5. a) Ta dễ chứng minh được ∆ ADE = ∆ CFE (c.g.c). Suy ra AD = CF=> BD = CF,
Nhận xét. Để chứng minh AP = AQ, ta thấy ∆ ABP và ∆ QCA có hai cặp cạnh bằng nhau nên ta tìm cách chứng tỏ cặp góc xen giữa bằng nhau.5. a) Ta dễ chứng minh được ∆ ADE = ∆ CFE (c.g.c). Suy ra AD = CF=> BD = CF, 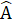 =
= 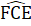 , mà hai góc ớ vị trí so le trong nên CF // AB.b) Xét ∆ BDC và ∆ FCD có: BD = FC (chứng minh trên);
, mà hai góc ớ vị trí so le trong nên CF // AB.b) Xét ∆ BDC và ∆ FCD có: BD = FC (chứng minh trên);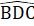 =
= 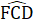 (do AB // CF); CD là cạnh chung.Do đó ∆ BDC = ∆ FCD.
(do AB // CF); CD là cạnh chung.Do đó ∆ BDC = ∆ FCD.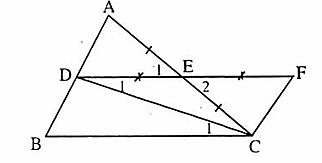 c) ∆ BDC = ∆ FCD (chứng minh trên) nên
c) ∆ BDC = ∆ FCD (chứng minh trên) nên 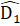 +
+ 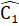 , mà hai góc ở vị trí so le trong suy ra DE // BC.a) Chứng minh tương tự bài 29 (SGK), ta có ∆ OAD= ∆ OCB.b) Xét ∆ ACB và ∆ CAD có:AC là cạnh chung;AD = CB (vì ∆ OAD = ∆ OCB);AB = CD (vì OB = OD, OA = OC). nên ∆ ACB= ∆ CAD (c.c.c).
, mà hai góc ở vị trí so le trong suy ra DE // BC.a) Chứng minh tương tự bài 29 (SGK), ta có ∆ OAD= ∆ OCB.b) Xét ∆ ACB và ∆ CAD có:AC là cạnh chung;AD = CB (vì ∆ OAD = ∆ OCB);AB = CD (vì OB = OD, OA = OC). nên ∆ ACB= ∆ CAD (c.c.c).