Học tốt Toán 7, Phần hình học, chương II, Bài 6. Tam giác cân
Giải Sách
2019-08-30T04:41:45-04:00
2019-08-30T04:41:45-04:00
https://baihochay.com/toan-hoc-7/hoc-tot-toan-7-phan-hinh-hoc-chuong-ii-bai-6-tam-giac-can-3766.html
/themes/linebox/images/no_image.gif
Bài học hay
https://baihochay.com/uploads/bai-hoc-hay-logo.png
Thứ sáu - 30/08/2019 04:39
Hệ thống kiến thức lí thuyết cần nhớ, hướng dẫn giải bài tập SGK Toán 7, Bài 6. Tam giác cân
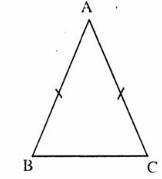
A. Tóm tắt kiến thức1. Tam giác câna) Định nghĩa. Tam giác cân là tam giác có hai cạnh bằng nhau∆ ABC cân tại A <=> 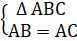 b) Tính chấtTrong tam giác cân, hai góc ở đáy bằng nhau∆ ABC cân tại A =>
b) Tính chấtTrong tam giác cân, hai góc ở đáy bằng nhau∆ ABC cân tại A => 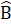 =
= 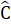 .
. c) Dấu hiệu nhận biết- Theo định nghĩa.- Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.2. Tam giác vuông câna) Định nghĩa. Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.∆ ABC vuông cân tại A <=>
c) Dấu hiệu nhận biết- Theo định nghĩa.- Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.2. Tam giác vuông câna) Định nghĩa. Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.∆ ABC vuông cân tại A <=> 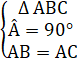
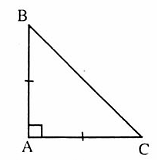 b)Tính chất. Mỗi góc nhọn của tam giác vuông cân bằng 45°.
b)Tính chất. Mỗi góc nhọn của tam giác vuông cân bằng 45°.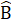 =
= 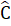 = 45°.3. Tam giác đềua) Định nghĩa. Tam giác đều là tam giác có ba cạnh bàng nhau.b) Tính chất. Trong tam giác đều, mỗi góc bằng 60oc) Dấu hiệu nhận biết- Theo định nghĩa.- Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.- Nếu một tam giác cân có một góc bằng 60° thì tam giác đó là tam giác đều.
= 45°.3. Tam giác đềua) Định nghĩa. Tam giác đều là tam giác có ba cạnh bàng nhau.b) Tính chất. Trong tam giác đều, mỗi góc bằng 60oc) Dấu hiệu nhận biết- Theo định nghĩa.- Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.- Nếu một tam giác cân có một góc bằng 60° thì tam giác đó là tam giác đều.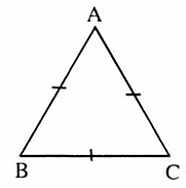 B. Ví dụ giải toánVí dụ. a) Một tam giác cân có một góc là 70°. Số đo của hai góc còn lại là bao nhiêu?b) Một tam giác cân có một góc là 96°. Số đo của hai góc còn lại là bao nhiêu?Giải. a) Nếu góc ở đỉnh tam giác cân là 70°, thì mỗi góc ở đáy tam giác cân bằng:
B. Ví dụ giải toánVí dụ. a) Một tam giác cân có một góc là 70°. Số đo của hai góc còn lại là bao nhiêu?b) Một tam giác cân có một góc là 96°. Số đo của hai góc còn lại là bao nhiêu?Giải. a) Nếu góc ở đỉnh tam giác cân là 70°, thì mỗi góc ở đáy tam giác cân bằng: 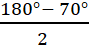 = 55°Nếu mỗi góc ở đáy tam giác cân là 70° thì góc ở đỉnh tam giác cân bằng: 180°-70°-70° = 40°.b) Nếu góc ở đáy tam giác cân là 96° thì tổng hai góc ở đáy là:96° +96° = 192° > 180° (không xảy ra).Do đó góc ở đỉnh tam giác cân là 96° thì mỗi góc ở đáy tam giác cân bằng
= 55°Nếu mỗi góc ở đáy tam giác cân là 70° thì góc ở đỉnh tam giác cân bằng: 180°-70°-70° = 40°.b) Nếu góc ở đáy tam giác cân là 96° thì tổng hai góc ở đáy là:96° +96° = 192° > 180° (không xảy ra).Do đó góc ở đỉnh tam giác cân là 96° thì mỗi góc ở đáy tam giác cân bằng 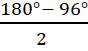 = 42°Nhận xét. Bài toán này dễ sót các trường hợp. Khi đề bài chưa cho cụ thể số đo đó là số đo góc ở đính hay ớ đáy, ta cần xét hai trường hợp.C. Hướng dẫn giải bài tập trong sách giáo khoaBài 46. (Bạn đọc tự vẽ hình)a) - Vẽ đoạn thẳng AC = 3cm.- Vẽ cung tròn tâm A bán kính 4cm và cung tròn tàm c bán kính 4cm, chúng cắt nhau tại B.Vẽ các đoạn thẳng AB, BC.b) - Vẽ đoạn thẳng BC - 3cm.Vẽ cung tròn tâm B bán kính 3cm và cung tròn tâm C bán kính 3cm, chúng cắt nhau tại A. Vẽ các đoạn thẳng AB, AC.Bài 47. Hình 116 (SGK). ∆ ABD cân tại A, ∆ ACE cân tại A.Hình 117 (SGK). ∆ GHI cân tại I.Hình 118 (SGK). ∆ OMN là tam giác đều.∆ OMK cân tại M, ∆ ONP cân tại N.∆ OKP cân tại O (vì
= 42°Nhận xét. Bài toán này dễ sót các trường hợp. Khi đề bài chưa cho cụ thể số đo đó là số đo góc ở đính hay ớ đáy, ta cần xét hai trường hợp.C. Hướng dẫn giải bài tập trong sách giáo khoaBài 46. (Bạn đọc tự vẽ hình)a) - Vẽ đoạn thẳng AC = 3cm.- Vẽ cung tròn tâm A bán kính 4cm và cung tròn tàm c bán kính 4cm, chúng cắt nhau tại B.Vẽ các đoạn thẳng AB, BC.b) - Vẽ đoạn thẳng BC - 3cm.Vẽ cung tròn tâm B bán kính 3cm và cung tròn tâm C bán kính 3cm, chúng cắt nhau tại A. Vẽ các đoạn thẳng AB, AC.Bài 47. Hình 116 (SGK). ∆ ABD cân tại A, ∆ ACE cân tại A.Hình 117 (SGK). ∆ GHI cân tại I.Hình 118 (SGK). ∆ OMN là tam giác đều.∆ OMK cân tại M, ∆ ONP cân tại N.∆ OKP cân tại O (vì 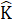 =
= 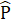 = 30° ).∆ OMN là tam giác cân (vì tam giác đều cũng là tam giác cân).Bài 48. Các bước tiến hành:- Cắt tấm bìa hình tam giác cân.- Gấp tấm bìa đó sao cho hai cạnh bên trùng nhau.- Quan sát phần cạnh đáy sau khi gấp lại chúng trùng nhau. Vậy hai góc ở đáy của tam giác cân bằng nhau.Bài 49. a) Gọi ABC là tam giác cân đã cho và góc ở đỉnh  = 40° .Ta có:
= 30° ).∆ OMN là tam giác cân (vì tam giác đều cũng là tam giác cân).Bài 48. Các bước tiến hành:- Cắt tấm bìa hình tam giác cân.- Gấp tấm bìa đó sao cho hai cạnh bên trùng nhau.- Quan sát phần cạnh đáy sau khi gấp lại chúng trùng nhau. Vậy hai góc ở đáy của tam giác cân bằng nhau.Bài 49. a) Gọi ABC là tam giác cân đã cho và góc ở đỉnh  = 40° .Ta có: 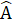 + 2
+ 2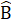 = 180° hay 2
= 180° hay 2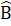 = 180°- 40° = 140°Do đóB
= 180°- 40° = 140°Do đóB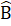 = 70°. Vậy
= 70°. Vậy 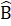 =
= 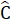 = 70°.b) Ta có: Â +
= 70°.b) Ta có: Â +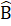 +
+ 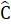 = 180° mà
= 180° mà 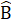 =
= 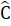 = 40° nên  + 2
= 40° nên  + 2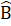 = 180°, hay  + 80° = 180°. Vậy  = 100°.Nhận xét. Trong tam giác cân, nếu biết số đo của một góc thì luôn tính được số đo hai góc còn lại.Bài 50. Ta có: AB = AC nên tam giác ABC cân tại A. Do đó
= 180°, hay  + 80° = 180°. Vậy  = 100°.Nhận xét. Trong tam giác cân, nếu biết số đo của một góc thì luôn tính được số đo hai góc còn lại.Bài 50. Ta có: AB = AC nên tam giác ABC cân tại A. Do đó 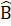 =
= 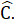 Trong ∆ ABC có: Â +
Trong ∆ ABC có: Â +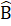 +
+ 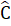 = 180° mà
= 180° mà 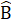 =
= 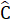 nên  + 2
nên  + 2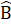 = 180°, hay 2
= 180°, hay 2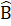 = 180°- Â. Suy ra
= 180°- Â. Suy ra 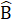 =
= 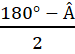 .Với  = 145° ta được:
.Với  = 145° ta được: 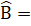
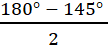 = 17,5° . Vậy
= 17,5° . Vậy 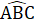 = 17,5°.Với  = 100° ta được :
= 17,5°.Với  = 100° ta được : 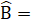
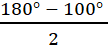 = 40°. Vậy ABC
= 40°. Vậy ABC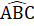 = 40° .Bài 51. a) ∆ ABD = ∆ ACE (c.g.c) suy ra
= 40° .Bài 51. a) ∆ ABD = ∆ ACE (c.g.c) suy ra 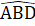 =
= 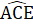 tức là
tức là 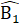 =
= 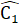 ∆ ABC cân tại A =>
∆ ABC cân tại A => 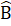 =
= 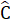 .Suy ra
.Suy ra 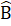 -
- 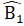 =
= 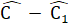 , do đó
, do đó 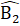 =
= 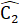 ∆ IBC có
∆ IBC có 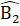 =
= 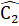 nên là tam giác cân tại I.
nên là tam giác cân tại I.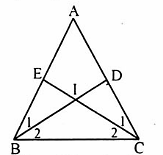 Bài 52. ∆ AOB = ∆ AOC (cạnh huyền - góc nhọn). Suy ra AB = AC, tức là∆ ABC cân Ta có:
Bài 52. ∆ AOB = ∆ AOC (cạnh huyền - góc nhọn). Suy ra AB = AC, tức là∆ ABC cân Ta có: 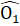 =
= 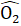 = 60o nên Â1 =Â2 = 30o, suy ra
= 60o nên Â1 =Â2 = 30o, suy ra 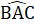 = 60oTam giác ABC cân có
= 60oTam giác ABC cân có 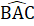 = 60o nên là tam giác đều.
= 60o nên là tam giác đều.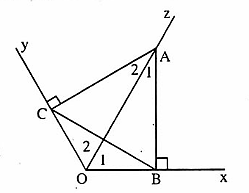 D. Bài tập luyện thêm1. Tìm x trong hình sau:
D. Bài tập luyện thêm1. Tìm x trong hình sau: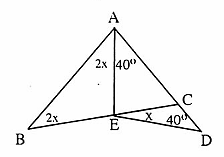 2. Tìm x trong hình bên, biết rằng Az // BC
2. Tìm x trong hình bên, biết rằng Az // BC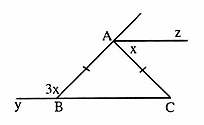 3. Cho ∆ ABC có
3. Cho ∆ ABC có 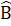 =
= 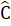 = 40°. Kẻ BD là tia phân giác của góc B (D ∈ AC). Chứng minh AD + BD = BC.4. Cho ∆ ABC có
= 40°. Kẻ BD là tia phân giác của góc B (D ∈ AC). Chứng minh AD + BD = BC.4. Cho ∆ ABC có 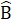 >
> 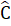 . Đường trung trực của cạnh BC cắt AC tại D. Kẻ AH ⊥ BC tại H, AH cắt BD tại E. Chứng minh ∆ ADE cân.5. Cho ∆ ABC có M là trung điểm BC. Biết rằng AM là phân giác góc BAC. Chứng minh ∆ ABC cân.6. Cho ∆ ABC có các tia phân giác trong của góc B và c cắt nhau tại I. Qua I kẻ đường thang song song với BC cắt AB, AC tại D và E.Chứng minh BD + CE = DE.Lời giải - Hướng dẫn - Đáp số∆ AED có
. Đường trung trực của cạnh BC cắt AC tại D. Kẻ AH ⊥ BC tại H, AH cắt BD tại E. Chứng minh ∆ ADE cân.5. Cho ∆ ABC có M là trung điểm BC. Biết rằng AM là phân giác góc BAC. Chứng minh ∆ ABC cân.6. Cho ∆ ABC có các tia phân giác trong của góc B và c cắt nhau tại I. Qua I kẻ đường thang song song với BC cắt AB, AC tại D và E.Chứng minh BD + CE = DE.Lời giải - Hướng dẫn - Đáp số∆ AED có 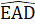 =
= 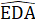 = 40° nên nó là tam giác cân.Suy ra
= 40° nên nó là tam giác cân.Suy ra 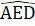 = 180° - 2.40° = 100°.∆ AEB cân tại E, theo tính chất góc ngoài tam giác:
= 180° - 2.40° = 100°.∆ AEB cân tại E, theo tính chất góc ngoài tam giác: 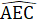 = 2.
= 2.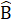 = 4x ,Suy ra 4x + x = 100°, do đó x = 20°.Az // BC nên
= 4x ,Suy ra 4x + x = 100°, do đó x = 20°.Az // BC nên 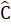 = x (hai góc so le trong).∆ ABC cân nên
= x (hai góc so le trong).∆ ABC cân nên 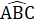 =
= 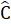 = x .Mặt khác,
= x .Mặt khác, 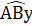 +
+ 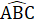 = 180° (hai góc kề bù) hay 3x + x = 180°=> x = 45°.3. ∆ ABC có
= 180° (hai góc kề bù) hay 3x + x = 180°=> x = 45°.3. ∆ ABC có 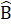 =
= 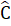 = 40° nên  = 100° .Trên BC lấy các điểm E, F sao cho BE = BA, BF = BD.Ta có ∆ BAD = ∆ BED (c.g.c).Suy ra AD = DE,
= 40° nên  = 100° .Trên BC lấy các điểm E, F sao cho BE = BA, BF = BD.Ta có ∆ BAD = ∆ BED (c.g.c).Suy ra AD = DE, 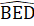 =  = 100° nên D = 80°.∆ BDF cân tại B và
= Â = 100° nên D = 80°.∆ BDF cân tại B và 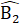 = 20° nên
= 20° nên 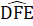 = 80° . Do đó ∆ DEF cân tại D,suy ra DE = DF.∆ DFC có C = 40° ;
= 80° . Do đó ∆ DEF cân tại D,suy ra DE = DF.∆ DFC có C = 40° ; 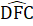 = 100° nên
= 100° nên 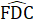 = 40°, hay ∆ DFC cân tại F,suy ra DF = FC. Suy ra AD = FC (= DE = DF).Vậy AD + BD = CF + FB = BC.
= 40°, hay ∆ DFC cân tại F,suy ra DF = FC. Suy ra AD = FC (= DE = DF).Vậy AD + BD = CF + FB = BC.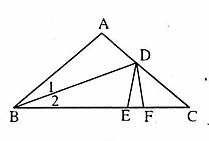 4.
4. 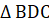 cân nên
cân nên 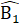 =
= 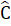 ∆ HAC và ∆ BEH là tam giác vuông tại H nên Â1 +
∆ HAC và ∆ BEH là tam giác vuông tại H nên Â1 + 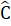 = 90o,
= 90o, 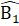 +
+ 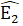 = 90o
= 90o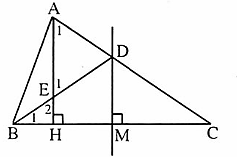 Suy ra Â1 = Â2Ta lại có Ê2 = Ê1 do đó Â1 = Ê1 hay ∆ ADE cân.5. Trên tia đối của tia MA lấy diểm D sao cho MD = MA.Xét ∆ ABMvà ∆ DCMcó:MB = MC (giả thiết);
Suy ra Â1 = Â2Ta lại có Ê2 = Ê1 do đó Â1 = Ê1 hay ∆ ADE cân.5. Trên tia đối của tia MA lấy diểm D sao cho MD = MA.Xét ∆ ABMvà ∆ DCMcó:MB = MC (giả thiết); 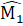 =
= 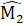 (đối đính); AM = MD.Do đó ∆ AMB = ∆ DMC (c.g.c) nên AB = DC,
(đối đính); AM = MD.Do đó ∆ AMB = ∆ DMC (c.g.c) nên AB = DC, 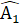 =
= 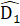 Mặt khác Â1 = Â2 suy ra
Mặt khác Â1 = Â2 suy ra 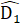 = Â2 hay ∆ ACD cân tại C=> AC = CD => AC = AB .Vậy ∆ ABC cân.Nhận xét. Để chứng minh ∆ ABC cân ta chưa tìm được cách nào trực tiếp để chứng minh cặp cạnh bằng nhau hoặc cặp góc bằng nhau, cũng như vận dụng BM = CM. Vì vậy việc kẻ thêm đường phụ là điều cần thiết.
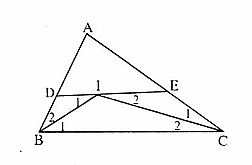
= Â2 hay ∆ ACD cân tại C=> AC = CD => AC = AB .Vậy ∆ ABC cân.Nhận xét. Để chứng minh ∆ ABC cân ta chưa tìm được cách nào trực tiếp để chứng minh cặp cạnh bằng nhau hoặc cặp góc bằng nhau, cũng như vận dụng BM = CM. Vì vậy việc kẻ thêm đường phụ là điều cần thiết.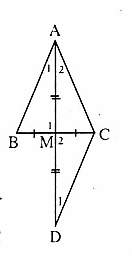 6. DE // BC nên
6. DE // BC nên 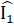 =
= 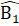 ;
; 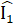 =
= 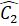 .Ta lại có
.Ta lại có 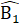 =
= 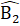 (giả thiết),
(giả thiết),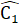 =
= 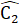 (giả thiết), suy ra
(giả thiết), suy ra 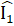 =
= 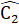 ;
; 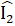 =
= 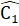 Do đó ∆ DIB cân tại D, ∆ EIC cân tại E, suy ra DI = BD, EI = CE.Vậy DE = DI + IE = BD + CE.Nhận xét. Việc phát hiện ra các tam giác cân và sử dụng tính chất của nó rất có lợi cho việc chứng minh các đoạn thắng bằng nhau.
Do đó ∆ DIB cân tại D, ∆ EIC cân tại E, suy ra DI = BD, EI = CE.Vậy DE = DI + IE = BD + CE.Nhận xét. Việc phát hiện ra các tam giác cân và sử dụng tính chất của nó rất có lợi cho việc chứng minh các đoạn thắng bằng nhau.