Giải sách bài tập Toán 8 - Diện tích tam giác
Giải Sách
2019-10-24T13:41:33-04:00
2019-10-24T13:41:33-04:00
https://baihochay.com/index.php/toan-hoc-8/giai-sach-bai-tap-toan-8-dien-tich-tam-giac-4061.html
/themes/linebox/images/no_image.gif
Bài học hay
https://baihochay.com/uploads/bai-hoc-hay-logo.png
Thứ năm - 24/10/2019 13:41
Hướng dẫn giải chi tiết bài tập trong sách bài tập Toán 8, tập 1, Phần II. Hình học, Chương II. Đa giác – diện tích đa giác. §3. Diện tích tam giác
A. Giải bài tập
25. Hai đường chéo của hình chừ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không? Vì sao?
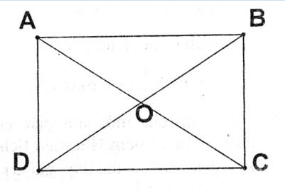 Giải: Gọi O là giao điểm 2 đường chéo hình chữ nhật ABCD.
=> OA = OB = OC = OD (tính chất hình chữ nhật)
Giải: Gọi O là giao điểm 2 đường chéo hình chữ nhật ABCD.
=> OA = OB = OC = OD (tính chất hình chữ nhật)
 OAB =
OAB =  OCD (c.g.c) => SOAB = SOCD ( 1)
OCD (c.g.c) => SOAB = SOCD ( 1)
 OAD =
OAD =  OBC (c.g.c) => SOAD = SOBC (2)
Kẻ AH ⊥ BD
SOAD =
OBC (c.g.c) => SOAD = SOBC (2)
Kẻ AH ⊥ BD
SOAD =  AH . OD
SOAB=
AH . OD
SOAB=  AH . OB
Suy ra : SOAD = SOAB (3)
Từ (1), (2) và (3) suy ra : SOAB - SOBC – SOCD = SODA
26. Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên đường thẳng d cố định song song với BC. Chứng minh rằng tam giác ABC có diện tích không đổi.
AH . OB
Suy ra : SOAD = SOAB (3)
Từ (1), (2) và (3) suy ra : SOAB - SOBC – SOCD = SODA
26. Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên đường thẳng d cố định song song với BC. Chứng minh rằng tam giác ABC có diện tích không đổi.
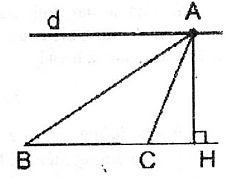 Giải:
Giải:  ABC có cạnh đáy BC không đổi, chiều cao AH là khoáng cách giữa 2 đường thằng song song không đổi. Vậy điểm A thay đổi trên đường thẳng d // BC thì SABC không đổi.
27. Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (d ⊥ BC).Gọi H là chân đường cao hạ từ đỉnh A đến đường thẳng BC.
a/ Điền vào ô trống bảng sau
b/ Vẽ đồ thị biểu diễn số đo SABC theo độ dài AH;
c/ Diện tích tam giác tỉ lệ thuận với chiều cao AH không ?
Giải: a/ Điền vào ô trống
ABC có cạnh đáy BC không đổi, chiều cao AH là khoáng cách giữa 2 đường thằng song song không đổi. Vậy điểm A thay đổi trên đường thẳng d // BC thì SABC không đổi.
27. Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (d ⊥ BC).Gọi H là chân đường cao hạ từ đỉnh A đến đường thẳng BC.
a/ Điền vào ô trống bảng sau
b/ Vẽ đồ thị biểu diễn số đo SABC theo độ dài AH;
c/ Diện tích tam giác tỉ lệ thuận với chiều cao AH không ?
Giải: a/ Điền vào ô trống
| Độ dài AH(cm) |
1 |
2 |
3 |
4 |
5 |
10 |
15 |
20 |
| SABC (cm2) |
2 |
4 |
6 |
8 |
10 |
20 |
30 |
40 |
b/ SABC là hàm số của chiều cao AH.
Gọi y là diện tích của  ABC (cm) và x là độ dài AH (cm) thì y = 2x
Ta có đồ thị như hình bên.
c/ Diện tích của tam giác tỉ lệ thuận với chiều cao.
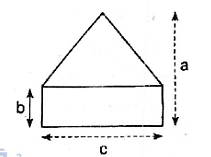
28. Tính diện tích hình bên theo kích thước đã cho trên hình.
ABC (cm) và x là độ dài AH (cm) thì y = 2x
Ta có đồ thị như hình bên.
c/ Diện tích của tam giác tỉ lệ thuận với chiều cao.
28. Tính diện tích hình bên theo kích thước đã cho trên hình.
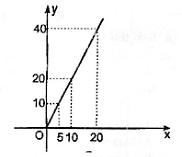 Giải: Diện tích phần là hình chữ nhật :
S1 = bc (đvdt)
Diện tích phần hình tam giác :
S2 =
Giải: Diện tích phần là hình chữ nhật :
S1 = bc (đvdt)
Diện tích phần hình tam giác :
S2 =  c . (a – b) (đvdt)
Diện tích hình vẽ đó :
S = bc +
c . (a – b) (đvdt)
Diện tích hình vẽ đó :
S = bc +  (a - b) (đvdt)
29. Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau: a/ 10 cm2;
b/ 15 cm2 ;
c/ 20 cm2
(a - b) (đvdt)
29. Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau: a/ 10 cm2;
b/ 15 cm2 ;
c/ 20 cm2
 Giải: Giả sử hai cạnh của tam giác là 5 cm và 6 cm. Chiều cao tương ứng của hai tam giác là h và k.
S1 =
Giải: Giả sử hai cạnh của tam giác là 5 cm và 6 cm. Chiều cao tương ứng của hai tam giác là h và k.
S1 =  . 5 . h; S2 =
. 5 . h; S2 =  . 6 . k
h và k là đường cao ứng với cạnh đáy là 5 và 6. Theo tính chất của đường vuông góc và đường xiên thì h ≤ 5 và k ≤ 6.
Suy ra diện tích của tam giác S ≤ 18.
Vậy diện tích của tam giác có thể bằng 10cm2 hay 15cm2 nhưng không thể bằng 20cm2.
30. Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ đỉnh B và C.
. 6 . k
h và k là đường cao ứng với cạnh đáy là 5 và 6. Theo tính chất của đường vuông góc và đường xiên thì h ≤ 5 và k ≤ 6.
Suy ra diện tích của tam giác S ≤ 18.
Vậy diện tích của tam giác có thể bằng 10cm2 hay 15cm2 nhưng không thể bằng 20cm2.
30. Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ đỉnh B và C.
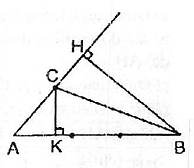 Giải: Ta có : SABC =
Giải: Ta có : SABC =  AB . CK =
AB . CK =  AC. BH
Suy ra : AB . CK = AC . BH
=>
AC. BH
Suy ra : AB . CK = AC . BH
=> 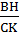 =
= 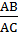 Mà AB = 3 AC (gt) =>
Mà AB = 3 AC (gt) => 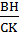 =
= 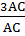 = 3
Vậy đường cao BH dài gấp 3 lần đường cao CK.
31. Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD thành ba đoạn thẳng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL. Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS.
Giải: Diện tích hình vuông ABCD bằng 6.6 = 36 (cm2)
Diện tích tam giác BEH bằng
= 3
Vậy đường cao BH dài gấp 3 lần đường cao CK.
31. Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD thành ba đoạn thẳng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL. Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS.
Giải: Diện tích hình vuông ABCD bằng 6.6 = 36 (cm2)
Diện tích tam giác BEH bằng 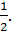 4.4 = 8 (cm2)
Diện tích tam giác DKN bằng
4.4 = 8 (cm2)
Diện tích tam giác DKN bằng  . 4.4 = 8 (cm2)
Diện tích phần còn lại là : 36 - (8 + 8) = 20 (cm2)
Trong tam giác vuông AEN ta có :
EN2 = AN2 + AE2 = 4 + 4 = 8
EN = 2
. 4.4 = 8 (cm2)
Diện tích phần còn lại là : 36 - (8 + 8) = 20 (cm2)
Trong tam giác vuông AEN ta có :
EN2 = AN2 + AE2 = 4 + 4 = 8
EN = 2 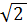 (cm)
Trong tam giác vuông BHE ta có :
EH2 = BE2 + BH2= 16+16 = 32
EH = 4
(cm)
Trong tam giác vuông BHE ta có :
EH2 = BE2 + BH2= 16+16 = 32
EH = 4 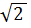 (cm)
Diện tích hình chữ nhật ENKH bằng 2
(cm)
Diện tích hình chữ nhật ENKH bằng 2 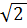 . 4
. 4 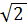 = 16 (cm2)
Nối đường chéo BD. Theo tính chất đường thẳng song song cách đều ta có hình chữ nhật ENKH chia thành 4 phần bằng nhau nên diện tích tứ giác PQRS chiếm 2 phần bằng 8 cm2 .
Diện tích tam giác AEN bằng
= 16 (cm2)
Nối đường chéo BD. Theo tính chất đường thẳng song song cách đều ta có hình chữ nhật ENKH chia thành 4 phần bằng nhau nên diện tích tứ giác PQRS chiếm 2 phần bằng 8 cm2 .
Diện tích tam giác AEN bằng  . 2.2 = 2 (cm2)
SAEPSN - SAEN + SEPSN - 2 + 4 - 6 (cm2)
B. GIẢI BÀI TẬP BỔ SUNG
a/ Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác thường thành ba mảnh để ghép lại được một hình chữ nhật hay không?
b/ Hãy chỉ một tam giác thành hai phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó.
c/ Hãy chia một tam giác thành 4 phần có diện tích bằng nhau bởi ba đường thẳng. trong đó chỉ có một đường đi qua đình của tam giác.
. 2.2 = 2 (cm2)
SAEPSN - SAEN + SEPSN - 2 + 4 - 6 (cm2)
B. GIẢI BÀI TẬP BỔ SUNG
a/ Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác thường thành ba mảnh để ghép lại được một hình chữ nhật hay không?
b/ Hãy chỉ một tam giác thành hai phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó.
c/ Hãy chia một tam giác thành 4 phần có diện tích bằng nhau bởi ba đường thẳng. trong đó chỉ có một đường đi qua đình của tam giác.
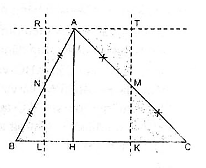 Giải: a/ Xét
Giải: a/ Xét  ABC. Kẻ đường cao AH. Gọi M là trung điểm của AC, N là trung điểm của AB.
Từ M kẻ đường thẳng song song AH cắt BC tại K.
Từ N kẻ đường thẳng song song AH cắt BC tại L.
Từ A kẻ đường thẳng song song với BC cắt hai đường thẳng MK và NL tại T và R.
Ta có:
ABC. Kẻ đường cao AH. Gọi M là trung điểm của AC, N là trung điểm của AB.
Từ M kẻ đường thẳng song song AH cắt BC tại K.
Từ N kẻ đường thẳng song song AH cắt BC tại L.
Từ A kẻ đường thẳng song song với BC cắt hai đường thẳng MK và NL tại T và R.
Ta có:  MKC =
MKC =  MTA
MTA
 NLB =
NLB =  NAR
Cắt
NAR
Cắt  ABC theo đường MK và NL ta ghép lại được một hình chữ nhật KTRL có diện tích bằng diện tích tam giác ABC.
b/ Ta đã biết hai tam giác có cạnh đáy bằng nhau và chung chiều cao thì có diện tích bằng nhau.
ABC theo đường MK và NL ta ghép lại được một hình chữ nhật KTRL có diện tích bằng diện tích tam giác ABC.
b/ Ta đã biết hai tam giác có cạnh đáy bằng nhau và chung chiều cao thì có diện tích bằng nhau.
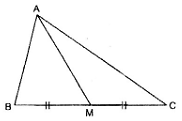 Giả sử
Giả sử  ABC. Gọi M là trung điểm của BC.
Cắt tam giác ABC theo đường AM chia tam giác ABC ra hai phần có diện tích bằng nhau.
c/ Tương tự như trên câu b.
ABC. Gọi M là trung điểm của BC.
Cắt tam giác ABC theo đường AM chia tam giác ABC ra hai phần có diện tích bằng nhau.
c/ Tương tự như trên câu b.
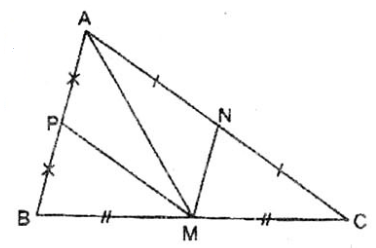 Xét
Xét  ABC. Gọi M là trung điểm của BC. N là trung điểm AC, P là trung điểm của AB.
Cắt tam giác ABC theo đường AM ta có hai phần có diện tích bằng nhau.
Cắt tam giác AMC theo đường AN ta có hai phần có diện tích bằng nhau.
Cắt tam giác AMB theo đường MP ta có hai phần có diện tích bằng nhau, ta có diện tích bốn phần chia bằng nhau.
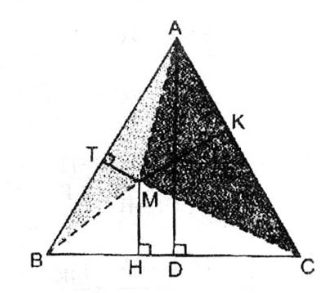
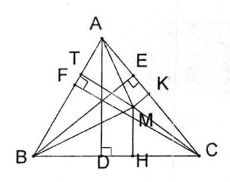
3.2 Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua M và vuông góc với AC tại điểm K. Đường thẳng đi qua M và vuông góc với AB tại điểm T. Chứng minh rằng MH + MK + MT không phụ thuộc vào vị trí của điểm M.
Giải:
Giả sử
ABC. Gọi M là trung điểm của BC. N là trung điểm AC, P là trung điểm của AB.
Cắt tam giác ABC theo đường AM ta có hai phần có diện tích bằng nhau.
Cắt tam giác AMC theo đường AN ta có hai phần có diện tích bằng nhau.
Cắt tam giác AMB theo đường MP ta có hai phần có diện tích bằng nhau, ta có diện tích bốn phần chia bằng nhau.
3.2 Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua M và vuông góc với AC tại điểm K. Đường thẳng đi qua M và vuông góc với AB tại điểm T. Chứng minh rằng MH + MK + MT không phụ thuộc vào vị trí của điểm M.
Giải:
Giả sử  ABC đều có cạnh bằng a, kẻ đường cao AD, đặt AD = h không đổi.
ABC đều có cạnh bằng a, kẻ đường cao AD, đặt AD = h không đổi.
 Ta có:
SMAB =
Ta có:
SMAB =  a. h
SMAC =
a. h
SMAC =  MK .a
SMBC =
MK .a
SMBC =  MH . a
SABC - SMAB + SMAC + SMBC
MH . a
SABC - SMAB + SMAC + SMBC
 a . h =
a . h =  MT . a +
MT . a +  MK . a +
MK . a +  MH . a
=
MH . a
=  a . (MT + MK + MH)
=> MT + MK + MH = h không đổi
Vậy tổng MT + MK + MH không phụ thuộc vào điểm M.
3.3 a/ Cho hai tam giác ABC và DBC. Kẻ đường cao của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi s là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC. Chứng minh rằng
a . (MT + MK + MH)
=> MT + MK + MH = h không đổi
Vậy tổng MT + MK + MH không phụ thuộc vào điểm M.
3.3 a/ Cho hai tam giác ABC và DBC. Kẻ đường cao của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi s là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC. Chứng minh rằng  =
= 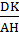 b/ Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó AD, BE, CF. Đường thẳng đi qua M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua M và song song với CF cắt cạnh BA tại điểm T.
Chứng minh rằng
b/ Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó AD, BE, CF. Đường thẳng đi qua M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua M và song song với CF cắt cạnh BA tại điểm T.
Chứng minh rằng 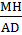 +
+ 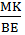 +
+ 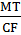 = 1
Giải: a/ Hai
= 1
Giải: a/ Hai  ABC và
ABC và  DBC có chung cạnh đáy BC nên ta có:
SABC =
DBC có chung cạnh đáy BC nên ta có:
SABC =  AH . BC = S
SDBC =
AH . BC = S
SDBC =  DK . BC = S’
Suy ra:
DK . BC = S’
Suy ra:  =
= 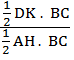 =
= 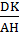 b/ Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S1, S2, S3.
Ta có:
S = S1 + S2 + S3
Trong đó: S =
b/ Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S1, S2, S3.
Ta có:
S = S1 + S2 + S3
Trong đó: S =  AD . BC =
AD . BC =  BE . AC =
BE . AC =  CF . AB
S1 =
CF . AB
S1 = 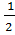 MT. AB
MT. AB
 S2 =
S2 = 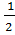 MK. AC
S3 =
MK. AC
S3 = 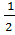 MH. BC
MH. BC
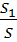 =
=  =
= 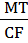
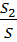 =
=  =
= 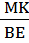
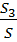 =
=  =
= 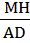 =>
=>