Giải sách bài tập Toán 8 - Tứ giác
Giải Sách
2019-10-16T12:01:10-04:00
2019-10-16T12:01:10-04:00
https://baihochay.com/toan-hoc-8/giai-sach-bai-tap-toan-8-tu-giac-3969.html
/themes/linebox/images/no_image.gif
Bài học hay
https://baihochay.com/uploads/bai-hoc-hay-logo.png
Thứ hai - 07/10/2019 12:47
Hướng dẫn giải chi tiết bài tập trong sách bài tập Toán 8, tập 1, Phần II. Hình học, Chương I. Tứ giác. §1. Tứ giác
A. Giải bài tập
1. Tính tổng các góc ngoài của tứ giác (tại mỗi đỉnh của tứ giác chì chọn một góc ngoài)
Â1 + 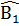 +
+  +
+ 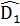 = 360°
(tổng các góc của tứ giác)
Tại mỗi đỉnh của tứ giác tổng một góc trong và một góc ngoài bằng 180° nên
= 360°
(tổng các góc của tứ giác)
Tại mỗi đỉnh của tứ giác tổng một góc trong và một góc ngoài bằng 180° nên
 Â1 + Â2 +
Â1 + Â2 + 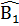 +
+ 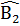 +
+ 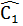 +
+ 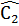 +
+ 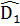 +
+ 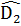 = 180°. 4 = 720°
=> Â1 +
= 180°. 4 = 720°
=> Â1 + 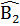 +
+  +
+  = 7200 – (Â1 +
= 7200 – (Â1 + 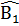 +
+ 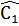 +
+  )
= 7200 – 3600 = 3600
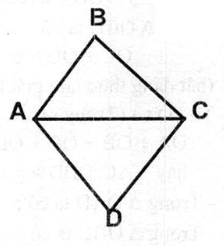
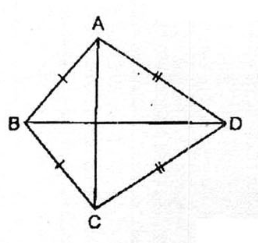
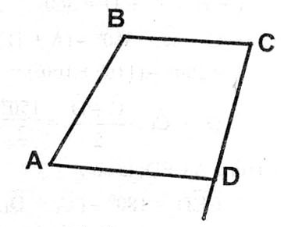
2. Tứ giác ABCD có AB = BC,CD = DA.
a/ Chứng minh rằng BD là đường trung trực của AC.
Cho biết
)
= 7200 – 3600 = 3600
2. Tứ giác ABCD có AB = BC,CD = DA.
a/ Chứng minh rằng BD là đường trung trực của AC.
Cho biết  = 100°,
= 100°, 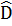 = 700, tính góc A và góc C.
Giải: a/ BA = BC (gt)
=> điểm B thuộc đường trung trực của AC
DA = DC (gt)
=> điểm D thuộc đường trung trực của AC
B và D là hai điểm phân biệt cùng thuộc đường trung trực của AC nên đường thẳng BD là đường trung trực của AC.
b/ Xét ∆ BAD và ∆ BCD. ta có:
BA = BC (gt)
DA = DC (gt)
BD cạnh chung
= 700, tính góc A và góc C.
Giải: a/ BA = BC (gt)
=> điểm B thuộc đường trung trực của AC
DA = DC (gt)
=> điểm D thuộc đường trung trực của AC
B và D là hai điểm phân biệt cùng thuộc đường trung trực của AC nên đường thẳng BD là đường trung trực của AC.
b/ Xét ∆ BAD và ∆ BCD. ta có:
BA = BC (gt)
DA = DC (gt)
BD cạnh chung
 do đó ∆ BAD = ∆ BCD (c.c.c) => BAD = BCD
do đó ∆ BAD = ∆ BCD (c.c.c) => BAD = BCD
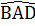 +
+  +
+ 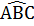 +
+  = 360°
= 360°
 +
+  = 360°-(
= 360°-(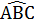 +
+ 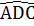 )
2
)
2 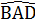 =360°- (100°+ 70°) = 190°
=>
=360°- (100°+ 70°) = 190°
=>  = 190° : 2 = 95°
=>
= 190° : 2 = 95°
=> 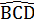 =
= 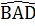 = 95°.
3. Học sinh tự vẽ.
4. Tính các góc của tứ giác ABCD. biết rằng : Â :
= 95°.
3. Học sinh tự vẽ.
4. Tính các góc của tứ giác ABCD. biết rằng : Â : 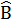 :
: 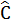 :
: 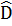 = 1:2:3:4
Giải: Theo bài ra ta có :
= 1:2:3:4
Giải: Theo bài ra ta có :
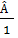 =
=  =
=  =
=  ; Â +
; Â +  +
+  = 3600
(tổng các góc của tứ giác)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
= 3600
(tổng các góc của tứ giác)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
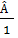 =
=  =
=  =
=  =
=  =
= 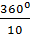 = 360
 = 1 . 36° = 36°
= 360
 = 1 . 36° = 36°
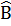 = 2. 36° = 72°
= 2. 36° = 72°
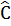 = 3.36°= 108°
= 3.36°= 108°
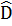 = 4.36° = 144°
5. Tứ giác ABCD có Â = 650,
= 4.36° = 144°
5. Tứ giác ABCD có Â = 650, 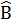 = 1170,
= 1170, 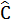 = 710. Tính số đo góc ngoài tại đỉnh D
Giải: Trong tứ giác ABCD ta có:
= 710. Tính số đo góc ngoài tại đỉnh D
Giải: Trong tứ giác ABCD ta có:
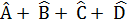 = 360°
(tổng các góc của tứ giác)
=>
= 360°
(tổng các góc của tứ giác)
=>  = 360°- (Â +
= 360°- (Â + 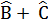 )
= 360°- (65°+ 117°+ 71°)= 107°
)
= 360°- (65°+ 117°+ 71°)= 107°
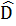 +
+ 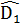 = 180° (2 góc kề bù)
=>
= 180° (2 góc kề bù)
=>  = 180° -
= 180° - 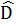 = 180° - 107° = 73°
= 180° - 107° = 73°
 6. Chứng minh rằng các góc của một tứ giác không thể đều là góc nhọn, không thể đều là góc tù.
Giải: Giả sử cả bốn góc của tứ giác đều là góc nhọn thì tổng bốn góc của tứ giác nhỏ hơn 360°, trái với tính chất tổng các góc của tứ giác bằng 360°. Vậy bốn góc của tứ giác không thể đều là góc nhọn. Giả sử cả bốn góc của tứ giác đều là góc tù thì tổng bốn góc của tứ giác lớn hơn 360°, trái với tính chất tổng các góc của tứ giác bằng 360°. Vậy bốn góc của tứ giác không thể đều là góc tù.
7. Cho tứ giác ABCD. Chứng minh rằng tổng hai góc ngoài tại các đỉnh A và C bằng tổng hai góc trong tại các đinh B và D.
Giải: Gọi Â1,
6. Chứng minh rằng các góc của một tứ giác không thể đều là góc nhọn, không thể đều là góc tù.
Giải: Giả sử cả bốn góc của tứ giác đều là góc nhọn thì tổng bốn góc của tứ giác nhỏ hơn 360°, trái với tính chất tổng các góc của tứ giác bằng 360°. Vậy bốn góc của tứ giác không thể đều là góc nhọn. Giả sử cả bốn góc của tứ giác đều là góc tù thì tổng bốn góc của tứ giác lớn hơn 360°, trái với tính chất tổng các góc của tứ giác bằng 360°. Vậy bốn góc của tứ giác không thể đều là góc tù.
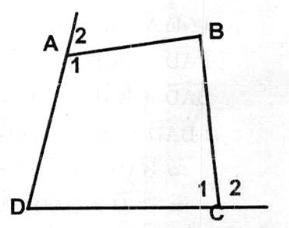
7. Cho tứ giác ABCD. Chứng minh rằng tổng hai góc ngoài tại các đỉnh A và C bằng tổng hai góc trong tại các đinh B và D.
Giải: Gọi Â1, 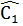 là góc trong của tứ giác tại đỉnh A và C. Â2,
là góc trong của tứ giác tại đỉnh A và C. Â2, 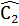 là góc ngoài tại đinh A và C.
Ta có : Â1 + Â2 = 180° (2 góc kề bù) => Â2 = 180° - Â1
là góc ngoài tại đinh A và C.
Ta có : Â1 + Â2 = 180° (2 góc kề bù) => Â2 = 180° - Â1
 +
+ 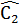 = 180° (2 góc kề bù)
=>
= 180° (2 góc kề bù)
=> 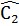 = 180° -
= 180° - 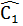 ,
,
 Suy ra: Â2 +
Suy ra: Â2 + 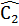 = 180° - Â1 + 180° -
= 180° - Â1 + 180° - 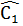 = 360°-(Â1 +
= 360°-(Â1 + 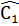 )
Trong tứ giác ABCD ta có :
)
Trong tứ giác ABCD ta có :
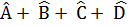 = 360° (tổng các góc của tứ giác)
=>
= 360° (tổng các góc của tứ giác)
=>  +
+ 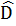 = 360° - (Â1 +
= 360° - (Â1 +  ) (2)
Từ (1) và (2) suy ra : Â2 +
) (2)
Từ (1) và (2) suy ra : Â2 + 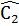 =
= 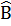 +
+ 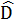 8. Tứ giác ABCD có Â = 110°.
8. Tứ giác ABCD có Â = 110°. 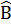 = 100°. Các tia phân giác của các góc C và D cắt nhau ở E .Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau tại F. Tính
= 100°. Các tia phân giác của các góc C và D cắt nhau ở E .Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau tại F. Tính 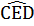 ,
, 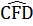 Giải: - Trong tứ giác ABCD, ta có :
Giải: - Trong tứ giác ABCD, ta có :
 = 360°
=>
= 360°
=> 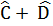 =360° - (Â+
=360° - (Â+ 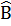 )
= 360°-(l10° + 100°)= 150°
)
= 360°-(l10° + 100°)= 150°
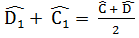 = 75°
- Trong ∆ CED, ta có :
= 75°
- Trong ∆ CED, ta có :
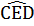 = 180°- (
= 180°- (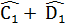 ) = 180° - 750 = 1050
DE ⊥ DF (tính chất tia phân giác của hai góc kề bù)
=>
) = 180° - 750 = 1050
DE ⊥ DF (tính chất tia phân giác của hai góc kề bù)
=> 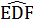 = 900
CE ⊥ CF(tính chất tia phân giác của hai góc kề bù)
=>
= 900
CE ⊥ CF(tính chất tia phân giác của hai góc kề bù)
=> 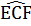 = 90°
= 90°
 Trong tứ giác CEDF, ta có :
Trong tứ giác CEDF, ta có :
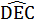 +
+ 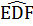 +
+  +
+ 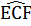 = 360°
=>
= 360°
=>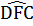 = 360° -(
= 360° -( 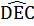 +
+ 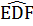 +
+  )
)
 = 360° -(105° + 90° + 90°) = 75°
9. Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn tổng hai cạnh đối.
Giải: Gọi O là giao điểm của hai đường chéo AC và BD.
Trong △ OAB, ta có :
= 360° -(105° + 90° + 90°) = 75°
9. Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn tổng hai cạnh đối.
Giải: Gọi O là giao điểm của hai đường chéo AC và BD.
Trong △ OAB, ta có :
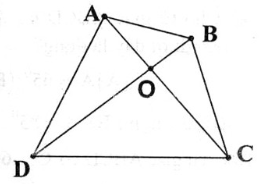 OA + OB > AB (bất đẳng thức tam giác) (1)
Trong △ OCD, ta có : OC + OD > CD (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2) :
OA + OB + OC + OD > AB + CD
=> AC + BD > AB + CD
10. Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác đó.
Giải: Đặt độ dài AB = a, BC = b, CD = c, AD = d
Gọi O là giao điểm hai đường chéo AC và BD
Trong △ OAB ta có :
OA + OB > AB (bất đẳng thức tam giác) (1)
Trong △ OCD, ta có : OC + OD > CD (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2) :
OA + OB + OC + OD > AB + CD
=> AC + BD > AB + CD
10. Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác đó.
Giải: Đặt độ dài AB = a, BC = b, CD = c, AD = d
Gọi O là giao điểm hai đường chéo AC và BD
Trong △ OAB ta có :
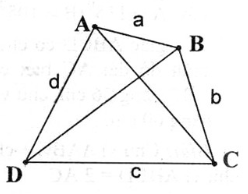 OA + OB > a (bất đẳng thức tam giác) (1)
Trong △ OCD ta có :
OC + OD > c (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra :
OA + OB + OC + OD > a + c
hay AC + BD > a + c (*)
Trong △ OAD ta có : OA + OD > d (bất đẳng thức tam giác) (3)
Trong △ OBC ta có : OB + OC > b (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra : OA + OD + OB + OC > b + d
=> AC + BD > b + d (**)
Từ (*) và (**) suy ra : 2 (AC + BD) >a + b + c + d
. =>AC + BD >
OA + OB > a (bất đẳng thức tam giác) (1)
Trong △ OCD ta có :
OC + OD > c (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra :
OA + OB + OC + OD > a + c
hay AC + BD > a + c (*)
Trong △ OAD ta có : OA + OD > d (bất đẳng thức tam giác) (3)
Trong △ OBC ta có : OB + OC > b (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra : OA + OD + OB + OC > b + d
=> AC + BD > b + d (**)
Từ (*) và (**) suy ra : 2 (AC + BD) >a + b + c + d
. =>AC + BD > 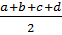 Trong △ ABC ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)
Trong △ ADC ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)
Suy ra : 2AC < a + b + c + d
AC <
Trong △ ABC ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)
Trong △ ADC ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)
Suy ra : 2AC < a + b + c + d
AC < 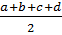 (5)
Trong △ ABD ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)
- Trong △ BCD ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)
Suy ra : 2BD < a + b + c + d
BD <
(5)
Trong △ ABD ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)
- Trong △ BCD ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)
Suy ra : 2BD < a + b + c + d
BD < 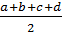 (6)
Từ (5) và (6) suy ra : AC + BD < a + b + c + d
B. Giải bài tập bổ sung
l.l Cho tứ giác ABCD có Â =
(6)
Từ (5) và (6) suy ra : AC + BD < a + b + c + d
B. Giải bài tập bổ sung
l.l Cho tứ giác ABCD có Â = 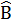 +10°,
+10°, 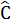 =
= 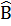 + 10°,
+ 10°,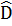 =
= 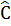 + 10° .Khẳng định nào dưới đây là đúng?
(A) Â = 65°;(B)
+ 10° .Khẳng định nào dưới đây là đúng?
(A) Â = 65°;(B) 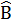 = 85°; (C)
= 85°; (C) 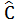 = 100°;(D)
= 100°;(D) 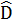 = 90°
Giải: Chọn ( B)
= 90°
Giải: Chọn ( B) 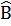 = 85°
1.2. Tứ giác ABCD có
= 85°
1.2. Tứ giác ABCD có  = 60°,
= 60°, 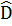 = 80°, -
= 80°, - 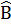 = 10° .Tính số đo các góc A và B. Chứng minh:  +
= 10° .Tính số đo các góc A và B. Chứng minh: Â + 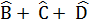 = 360° => Â +
= 360° => Â + 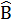 = 360° - (
= 360° - ( 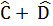 )
Giải: Â +
)
Giải: Â + 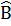 = 360° - (60° + 80°) = 220°
 -
= 360° - (60° + 80°) = 220°
 -  = 10°
Vậy  = 115°;
= 10°
Vậy  = 115°;  = 105°
1.3 Tứ giác ABCD có chu vi bằng 66cm. Tính độ dài AC biết chu vi tam giác ABC bằng 56 cm. chu vi tam giác ACD bằng 60 cm.
Giải: Chu vi △ABC + chu vi △ACD -
chu vi △BCD = 2 AC
=> 2 AC = 56 + 60 - 66 = 50 (cm)
AC = 25 (cm)
= 105°
1.3 Tứ giác ABCD có chu vi bằng 66cm. Tính độ dài AC biết chu vi tam giác ABC bằng 56 cm. chu vi tam giác ACD bằng 60 cm.
Giải: Chu vi △ABC + chu vi △ACD -
chu vi △BCD = 2 AC
=> 2 AC = 56 + 60 - 66 = 50 (cm)
AC = 25 (cm)