A - Mục đích, yêu cầu
- HS thiết lập được màn hình chính và phân biệt được cách nhập lệnh từ cửa sổ CAS của GeoGebra.
- HS hiểu và áp dụng được các tính năng của phần mềm trong việc học tập và giải toán trong chương trình học trên lớp của mình.
B - Những điểm cần lưu ý và gợi ý dạy học
a) Cần thiết lập các thông số ngầm định ban đầu để việc giảng dạy được thuận tiện, dễ dàng. Cụ thể cần thiết lập giao diện của GeoGebra như hình sau:
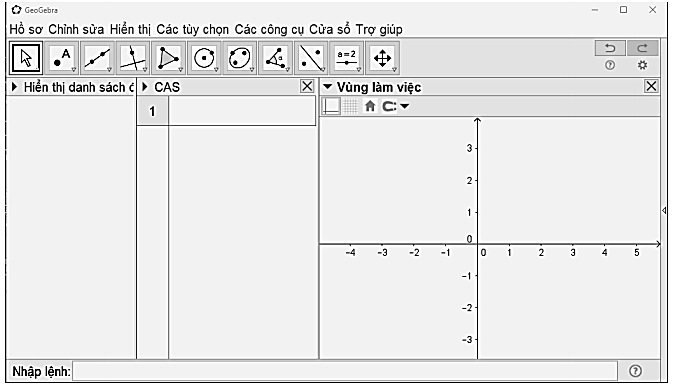
- Thiết lập để màn hình hiện ba cửa sổ cùng một lúc:
(1) Danh sách các đối tượng (bên trái).
(2) CAS (giữa)
(3) Cửa sổ làm việc chính 2D (phải).
- Thiết lập chế độ ngôn ngữ tiếng Việt và cỡ chữ đủ to để dễ quan sát.
- Chế độ hiển thị tên nên thiết lập là: Chỉ hiển thị tên các điểm mới như trong hình sau:
b) Chú ý trong cửa sổ CAS có hai chế độ thực hiện tính toán: chế độ tính toán
Chính xác ( nút = và chế độ tính toán gần đúng (nút ≈)
- Chế độ tính toán chính xác sẽ tính chính xác số hữu tỉ theo phân số và số thập phân.
Ví dụ:
- Chế độ tính toán gần đúng sẽ đưa tất cả kết quả về dạng số thập phân và thể hiện số thập phân theo lựa chọn của lệnh:
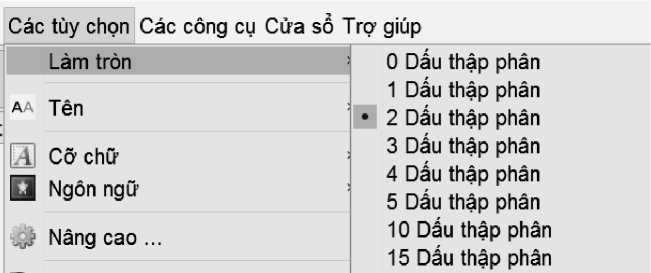
Ví dụ:

c) Đối với đa thức, đơn thức, biểu thức chứa chữ
Trong GeoGebra (làm việc với khung CAS), GV cần lưu ý nếu muốn sử dụng biến để tính toán trong biểu thức (đa thức) thì phải định nghĩa biến trước khi định nghĩa đa thức. Biến được định nghĩa trong CAS thì là biến trong tin học, có tên (ô nhớ) và giá trị có thể thay đổi. Giáo viên cần chú ý khái niệm biến trong GeoGebra khác với biến trong trong SGK Toán 7 tập hai, chương Biểu thức đại số.
Nếu không cần tính toán với các biến mà chỉ cần thực hiện các phép cộng, trừ, nhân, chia các đa thức thì cần lưu ý cách định nghĩa biến trong đa thức. Ví dụ chúng ta định nghĩa đa thức sau:
P := xyz + 2xy^2 + xyz^2
GeoGebra hiểu là đa thức này có hai biến là xyz, xy có thể lại viết trong toán học như sau P = X + 2Y2 + X2, ở đây X = xyz, Y = xy. Ta thấy GeoGebra hiểu xyz x*y*z, xy x*y nhưng nếu có số thì GeoGebra lại hiểu đó là phép nhân, ví dụ 2x thì hiểu là 2*x hay xy^2 thì hiểu là (xy)2, ở đây xy là một biến.
Sau khi định nghĩa như trên, và nhập tiếp: P + xyz + x^2y thì kết quả sẽ thu được là: 2xyz + x2y + 2xy2 + xyz2.
Nếu muốn định nghĩa đa thức với các biến x, y, z thì phải nhập các phép toán nhân hoặc dấu cách giữa các biến, chẳng hạn
P := x^2*y + x*y^2 hoặc P := x^2 y + xy^2 để định nghĩa đa thức P = x2y + xy2
Q := a*b*2c + a^2*c + b*c^2 hoặc Q := a b 2c + a^2 c + b c^2 để định nghĩa đa thức Q = 2abc + a2c + bc2
d) Đối với hàm: Hàm số có thể có 1, 2, 3, hoặc nhiều biến. Hàm là đối tượng toán học trong GeoGebra và cần được định nghĩa chính xác các biến.
Ngầm định, sau khi định nghĩa thì đồ thị của các hàm số một biến sẽ tự động hiển thị trên mặt phẳng làm việc (2D), đồ thị của hàm hai biến sẽ tự động hiển thị như một mặt trong không gian 3D.
Đối với HS lớp 7, GV chỉ nên giới thiệu hàm một biến. Tên các biến nên dùng là x, y.
e) Một số chú ý khi nhập biểu thức và số trong cửa sổ CAS.
| Nhập dữ liệu |
Ý nghĩa toán học thực sự |
Chú ý |
| a*b |
a x b |
a nhân b |
| a b |
a nhân b |
| 2a |
2 x a |
2 nhân a |
| ab |
kí hiệu ab |
kí hiệu ab chứ không phải là a nhân b |
| a2 |
kí hiệu a2 |
kí hiệu a2 chứ không phải là a nhân 2 |
| xy^2 |
Kí hiệu xy2chính là xy*xy |
xy là một biến |
| (xy)^2 |
f) Một số hàm có thể sử dụng trong cửa sổ CAS.
| Cú pháp lệnh |
Ý nghĩa |
| USCLN[m1, m2, ...] |
Tính ước số chung lớn nhất của các số m1, m2, |
GCN[m1, m2, ....]
| BSCNN[m1, m2, ...] |
Tính bội số chung nhỏ nhất của các số m1, m2, |
LCM[m1, m2, ....]
| DanhSachUocSo[m] |
Danh sách các ước số của m |
DivisorsList[m]
| UocSo[m] |
Đếm số các ước số của số m |
Divisors[m]
| isPrime[p] |
Kiểm tra p có phải là số nguyên tố hay không, trả lại giá trị true nếu p là số nguyên tố hoặc false nếu ngược lại. |
| Next Prime[p] |
Cho số nguyên số ngay sau số tự nhiên p. |
| Previous Prime[p] |
Cho số nguyên tố ngay trước số tự nhiên p. |
| Factor[m] |
Phân tích số tự nhiên m thành tích các thừa số nguyên tố. |
| Factor[<đa thức>] |
Khai triển đa thức thành tích các thừa số trong phạm vi các số hữu tỉ. |
| Factors[m] |
Trả lại dãy các số nguyên tố nằm trong khai triển |
| Factors[<đa thức>] |
m thành tích các thừa số này. |
| Expand[<đa thức> | <biểu thức>] |
Khai triển biểu thức đại số (đa thức). |
| Simplify[<đa thức> | <biểu thức>] |
Rút gọn biểu thức tính đại số (đa thức). |
| Div[<đa thức 1>, <đa thức 2>] |
Cho thương của phép chia đa thức 1 cho đa thức |
| Div[m1, m2] |
2 hoặc của số m1 cho số m2. |
| Mod[<đa thức 1>, <đa thức 2>] |
Cho dư của phép chia đa thức hoặc số. |
Mod[m1, m2]
| Cú pháp lệnh |
Ý nghĩa |
Division[<đa thức 1 >, <đa thức 2>]
Division[m1, m2] |
Cho thương và dư của phép chia đa thức hoặc số. |
g) Có thể thực hiện nội dung giảng dạy theo tiết như sau:
Tiết 1:
- Nhắc lại bài cũ, thiết lập các đối tượng số tự do. Ví dụ lệnh m := 1 sẽ tạo ra một đối tượng số tự do, đối tượng này có thể hiện trên màn hình làm việc chính.
- Thực hiện các tính toán chính xác với biểu thức chứa phân số.
Chú ý: trong phần học này sẽ phải dùng chế độ tính toán chính xác trong cửa sổ CAS. Nháy lên nút = để cài đặt chế độ tính toán chính xác.
Tiết 2:
- Thực hiện các phép tính với đơn thức, đa thức.
- Tính giá trị của đa thức.
- Cuối của tiết 1 GV có thể giảng về chế độ tính toán gần đúng trong CAS.
Tiết 3:
- Thực hiện các lệnh vẽ điểm (bằng công cụ điểm) hoặc lệnh trên mặt phẳng.
- Lệnh vẽ đồ thị hàm số, các dạng cơ bản.
- Thực hiện các lệnh tạo hàm số có phụ thuộc. Ví dụ:
m := 1
f(x) := m*x - 1
Khi đó hàm f(x) sẽ phụ thuộc toán học vào đối tượng m.
Tiết 4:
- Thực hiện các lệnh thay đổi thuộc tính, màu sắc, kiểu của điểm và đồ thị.
Hướng dẫn trả lời câu hỏi và bài tập
1. a) 32768/125
b) 12167/8000
c) 2197/3375
d) 2299/4320
2. xy2 + 6x2y - 2xy + 5
4. 4
5. 0,19
7. (B)