Học tốt Toán 7, Phần hình học, chương II, Bài 8. Các trường hợp bằng nhau của tam giác vuông
Giải Sách
2019-08-31T11:12:16-04:00
2019-08-31T11:12:16-04:00
https://baihochay.com/index.php/toan-hoc-7/hoc-tot-toan-7-phan-hinh-hoc-chuong-ii-bai-8-cac-truong-hop-bang-nhau-cua-tam-giac-vuong-3768.html
/themes/linebox/images/no_image.gif
Bài học hay
https://baihochay.com/uploads/bai-hoc-hay-logo.png
Thứ bảy - 31/08/2019 11:12
Hệ thống kiến thức lí thuyết cần nhớ, hướng dẫn giải bài tập SGK Toán 7, Bài 8. Các trường hợp bằng nhau của tam giác vuông
A. Tóm tắt kiến thứcNgoài các trường họp bằng nhau đã biết của hai tam giác vuông (hai cạnh góc vuông, một cạnh góc vuông và một góc nhọn kề cạnh ấy, cạnh huyền và một góc nhọn), còn có trường họp bằng nhau theo cạnh huyền - cạnh góc vuông.Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau.
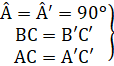 => ∆ ABC = ∆ A'B'C' (cạnh huyền – cạnh góc vuông)B. Ví dụ giải toánVí dụ. Cho ∆ ABC nhọn có AH ⊥ BC. Dựng ra phía ngoài tam giác ABC các ∆ ABD, ∆ ACE vuông cân tại B và C. Kẻ DI; EK vuông góc với đường thẳng BC. Chứng minh rằng:a) ∆ IBD= ∆ HAB.b) BI = CK.c) DI + EK = BC.
=> ∆ ABC = ∆ A'B'C' (cạnh huyền – cạnh góc vuông)B. Ví dụ giải toánVí dụ. Cho ∆ ABC nhọn có AH ⊥ BC. Dựng ra phía ngoài tam giác ABC các ∆ ABD, ∆ ACE vuông cân tại B và C. Kẻ DI; EK vuông góc với đường thẳng BC. Chứng minh rằng:a) ∆ IBD= ∆ HAB.b) BI = CK.c) DI + EK = BC.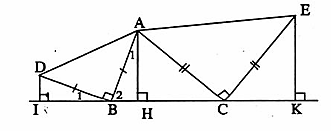 Giải a) ABD = 90° nên
Giải a) ABD = 90° nên 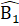 +
+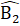 =90°.∆ ABH có H = 90° nên
=90°.∆ ABH có H = 90° nên 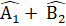 = 90° suy ra
= 90° suy ra 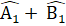 .∆ IBDvà ∆ HAB có:
.∆ IBDvà ∆ HAB có: 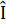 =
= 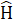 = 90o,
= 90o, 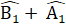 , BD=AB.Do đó ∆ IBD = ∆ HAB (cạnh huyển - góc nhọn).∆ IBD = ∆ HAB nên BI = AH.Chứng minh tương tự, ta có ∆ HAC = ∆KCE (cạnh huyền - góc nhọn)nên CK = AH. Do đó BI = CK (= AH).c) ∆ IBD = ∆ HAB nên DI = BH; ∆ HAC = ∆ KCE nên EK = CH.Suy ra DI + EK = BH + CH = BC.Nhận xét. Về phương pháp giải câu b), ta không thể chứng minh trực tiếp được mà dùng đoạn thẳng trung gian. Để chứng minh đoạn thẳng BC bằng tổng hai đoạn thẳng DI và EK, ta chia BC thành hai đoạn, rồi chứng minh một đoạn bằng DI, một đoạn bằng EK. Ưu tiên điếm có sẵn trong hình.C. Hướng dẫn giải bài tập trong sách giáo khoaBài 63. a) ∆ AHB = ∆ AHC (cạnh huyền - cạnh góc vuông)HB = HC.b) ∆ AHB = ∆ AHC =>
, BD=AB.Do đó ∆ IBD = ∆ HAB (cạnh huyển - góc nhọn).∆ IBD = ∆ HAB nên BI = AH.Chứng minh tương tự, ta có ∆ HAC = ∆KCE (cạnh huyền - góc nhọn)nên CK = AH. Do đó BI = CK (= AH).c) ∆ IBD = ∆ HAB nên DI = BH; ∆ HAC = ∆ KCE nên EK = CH.Suy ra DI + EK = BH + CH = BC.Nhận xét. Về phương pháp giải câu b), ta không thể chứng minh trực tiếp được mà dùng đoạn thẳng trung gian. Để chứng minh đoạn thẳng BC bằng tổng hai đoạn thẳng DI và EK, ta chia BC thành hai đoạn, rồi chứng minh một đoạn bằng DI, một đoạn bằng EK. Ưu tiên điếm có sẵn trong hình.C. Hướng dẫn giải bài tập trong sách giáo khoaBài 63. a) ∆ AHB = ∆ AHC (cạnh huyền - cạnh góc vuông)HB = HC.b) ∆ AHB = ∆ AHC => 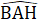 =
= 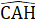 .
.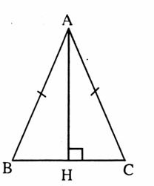 Bài 64. Bổ sung AB = DE thì ∆ ABC = ∆ DEF(c.g.c).Bổ sung
Bài 64. Bổ sung AB = DE thì ∆ ABC = ∆ DEF(c.g.c).Bổ sung 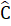 =
= 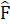 thì ∆ ABC = ∆ DEF (g.c.g).Bổ sung BC = EF thì ∆ ABC = ∆ DEF (cạnh huyền - cạnh góc vuông).Bài 65. a) ∆ ABH = ∆ ACK (cạnh huyền - góc nhọn)=> AH = AK.∆ AIH = ∆ AIK (cạnh huyền - cạnh góc vuông)=>
thì ∆ ABC = ∆ DEF (g.c.g).Bổ sung BC = EF thì ∆ ABC = ∆ DEF (cạnh huyền - cạnh góc vuông).Bài 65. a) ∆ ABH = ∆ ACK (cạnh huyền - góc nhọn)=> AH = AK.∆ AIH = ∆ AIK (cạnh huyền - cạnh góc vuông)=> 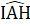 =
= 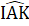 => AI là tia phân giác của góc A.
=> AI là tia phân giác của góc A.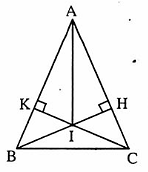 Bài 66. ∆ ADM = ∆ AEM (cạnh huyền - góc nhọn).Suy ra MD = ME, ∆ MDB = ∆ MEC (cạnh huyền - cạnh góc vuông).Ta còn suy ra: AD = AE, BD = CE nên AB = AC.Do đó ∆ AMB = ∆ AMC(c.c.c).D. Bài tập luyện thêm1. Cho ∆ ABC vuông tại A có AB < AC. Kẻ tia phân giác góc ABC cắt AC tại D. Kẻ DE vuông góc với BC tại E. Hai đường thắng BA và ED cắt nhau tại H. Chứng minh rằng:a) ∆ ABD= ∆ EBD.b) ∆ ADH = ∆ EDC.c) ∆ AHC= ∆ ECH.d) ∆ BEH = ∆ BAC.2. Cho ∆ ABC nhọn có AH là đường cao. Dựng ra phía ngoài tam giác ABC các tam giác ABD, ACE vuông cân tại A. Gọi I, K là chân đường vuông góc kẻ từ D, E xuống đường thẳng AH. Gọi o là giao điểm của DE với HK. Chứng minh rằng:a) ∆ IAD = ∆ HBA.b) DI = EK.c) OD = OE.3. Cho ∆ ABC cân ở A. Qua B vẽ đường thẳng vuông góc với AB. qua C vẽ đường thảng vuông góc với AC, hai đường thẳng này cắt nhau ở D. Chứng minh AD là tia phân giác góc BAC.4. Cho ∆ ABC cân ớ A. Trôn cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Từ D kẻ đường vuông góc với BC cắt AB ở M, từ E kẻ đường vuông góc với BC cắt AC ở N.a) Chứng minh MD = NE.b) MN cắt DE tại I. Chứng minh I là trung điểm của DE.Lời giải - Hướng dẫn - Đáp số1. a) ∆ ABD và ∆ EBDcó:
Bài 66. ∆ ADM = ∆ AEM (cạnh huyền - góc nhọn).Suy ra MD = ME, ∆ MDB = ∆ MEC (cạnh huyền - cạnh góc vuông).Ta còn suy ra: AD = AE, BD = CE nên AB = AC.Do đó ∆ AMB = ∆ AMC(c.c.c).D. Bài tập luyện thêm1. Cho ∆ ABC vuông tại A có AB < AC. Kẻ tia phân giác góc ABC cắt AC tại D. Kẻ DE vuông góc với BC tại E. Hai đường thắng BA và ED cắt nhau tại H. Chứng minh rằng:a) ∆ ABD= ∆ EBD.b) ∆ ADH = ∆ EDC.c) ∆ AHC= ∆ ECH.d) ∆ BEH = ∆ BAC.2. Cho ∆ ABC nhọn có AH là đường cao. Dựng ra phía ngoài tam giác ABC các tam giác ABD, ACE vuông cân tại A. Gọi I, K là chân đường vuông góc kẻ từ D, E xuống đường thẳng AH. Gọi o là giao điểm của DE với HK. Chứng minh rằng:a) ∆ IAD = ∆ HBA.b) DI = EK.c) OD = OE.3. Cho ∆ ABC cân ở A. Qua B vẽ đường thẳng vuông góc với AB. qua C vẽ đường thảng vuông góc với AC, hai đường thẳng này cắt nhau ở D. Chứng minh AD là tia phân giác góc BAC.4. Cho ∆ ABC cân ớ A. Trôn cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Từ D kẻ đường vuông góc với BC cắt AB ở M, từ E kẻ đường vuông góc với BC cắt AC ở N.a) Chứng minh MD = NE.b) MN cắt DE tại I. Chứng minh I là trung điểm của DE.Lời giải - Hướng dẫn - Đáp số1. a) ∆ ABD và ∆ EBDcó: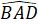 =
= 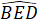 (= 90° ;
(= 90° ; 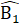 =
= 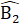 (giả thiết); BD là cạnh chung.Do đó ∆ ABD = ∆ EBD (cạnh huyền - góc nhọn),b) ∆ ADH và ∆ EDCcó:
(giả thiết); BD là cạnh chung.Do đó ∆ ABD = ∆ EBD (cạnh huyền - góc nhọn),b) ∆ ADH và ∆ EDCcó: 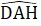 =
= 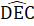 (=90°);
(=90°); 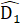 =
=  (đối đỉnh);AD = ED (vì ∆ ABD = ∆ EBD).Do đó ∆ ADH= ∆ EDC(g.c.g).
(đối đỉnh);AD = ED (vì ∆ ABD = ∆ EBD).Do đó ∆ ADH= ∆ EDC(g.c.g).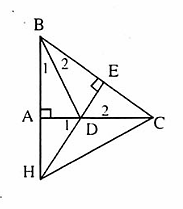 c) ∆ ADH = ∆ EDCsuy ra AH = EC, AD = DE, DC = DH=> AC = EH.Xét ∆ ACHvà ∆ EHCcó: HAC = CEH(= 90°); AH = CE; AC = EH.Do đó ∆ AHC= ∆ ECH.(c.g.c).d) Xét ∆ BEH và ∆ BAC có:
c) ∆ ADH = ∆ EDCsuy ra AH = EC, AD = DE, DC = DH=> AC = EH.Xét ∆ ACHvà ∆ EHCcó: HAC = CEH(= 90°); AH = CE; AC = EH.Do đó ∆ AHC= ∆ ECH.(c.g.c).d) Xét ∆ BEH và ∆ BAC có: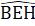 =
= 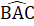 (=90°);
(=90°); 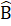 chung; EH = AC (∆ AHC = ∆ ECH).Suy ra ∆ BEH = ∆ BAC (cạnh góc vuông - góc nhọn).2. a) ∆ IDA và ∆ HAB có:
chung; EH = AC (∆ AHC = ∆ ECH).Suy ra ∆ BEH = ∆ BAC (cạnh góc vuông - góc nhọn).2. a) ∆ IDA và ∆ HAB có: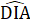 =
=  = 90°;AD = AB (giả thiết);Â1 =
= 90°;AD = AB (giả thiết);Â1 = 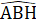 (cùng phụ với Â2 ).Do đó ∆ IAD = ∆ HBA (cạnh huyền - góc nhọn),
(cùng phụ với Â2 ).Do đó ∆ IAD = ∆ HBA (cạnh huyền - góc nhọn),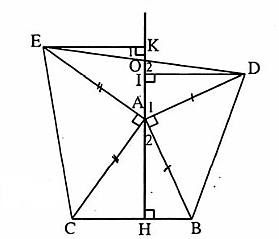 b) ∆ IAD = ∆ HBA nên DI =AH.Chứng minh tương tự, ta có ∆ KAE = ∆ HCA nên EK = AH.Do đó DI = EK.∆ DO và ∆ KEO có:
b) ∆ IAD = ∆ HBA nên DI =AH.Chứng minh tương tự, ta có ∆ KAE = ∆ HCA nên EK = AH.Do đó DI = EK.∆ DO và ∆ KEO có: 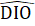 =
= 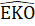 = 90° ; DI = EK (chứng minh trên); Ô1 = Ô2 (đối đinh).Do đó ∆ IDO = ∆ KEO, suy ra OD = OE.3. Xét ∆ ABD và ∆ ACD có:
= 90° ; DI = EK (chứng minh trên); Ô1 = Ô2 (đối đinh).Do đó ∆ IDO = ∆ KEO, suy ra OD = OE.3. Xét ∆ ABD và ∆ ACD có: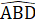 =
= 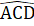 = 90°;AB = AC (giả thiết);AD là cạnh chung.Suy ra ∆ ABD = ∆ ACD (cạnh huyền - cạnh góc vuông) do đó Â1 = Â2 , suy ra AD là tia phân giác của góc BAC.4. a) ∆ BDMvà ∆ CENcó:
= 90°;AB = AC (giả thiết);AD là cạnh chung.Suy ra ∆ ABD = ∆ ACD (cạnh huyền - cạnh góc vuông) do đó Â1 = Â2 , suy ra AD là tia phân giác của góc BAC.4. a) ∆ BDMvà ∆ CENcó: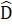 = Ê = 90° ;
= Ê = 90° ; 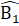 =
= 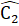 (=
(=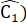 ; BD = CE (giả thiết).Nên ∆ BDM = ∆ CEN (g.c.g).Suy ra DM = EN.
; BD = CE (giả thiết).Nên ∆ BDM = ∆ CEN (g.c.g).Suy ra DM = EN.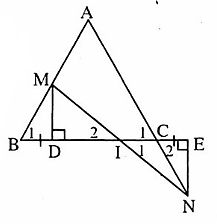 b) ∆ DMI và ∆ ENI có:
b) ∆ DMI và ∆ ENI có: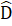 = Ê = 90° ;MD = EN (chứng minh trên);
= Ê = 90° ;MD = EN (chứng minh trên);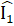 =
= 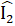 (đối đỉnh);nên ∆ DMI - ∆ ENI (g.c.g).Do đó DI = EI suy ra I là trung điểm của DE.Nhận xét- Câu b) giải được có sử dụng kết quả của câu a). Vì vậy những bài có nhiều câu hỏi, ta nên chú ý khai thác ý của câu trước để phục vụ hiệu quả cho câu sau.- Nếu bỏ điểm D và E ở giả thiết và câu hỏi a, thì câu b là câu khó.- Nếu vận dụng định lí Py-ta-go, ta có thể thấy rằng cạnh huyền của tam giác vuông là cạnh lớn nhất, thì ta có câu hay và khó là: Chứng minh MN > BC.
(đối đỉnh);nên ∆ DMI - ∆ ENI (g.c.g).Do đó DI = EI suy ra I là trung điểm của DE.Nhận xét- Câu b) giải được có sử dụng kết quả của câu a). Vì vậy những bài có nhiều câu hỏi, ta nên chú ý khai thác ý của câu trước để phục vụ hiệu quả cho câu sau.- Nếu bỏ điểm D và E ở giả thiết và câu hỏi a, thì câu b là câu khó.- Nếu vận dụng định lí Py-ta-go, ta có thể thấy rằng cạnh huyền của tam giác vuông là cạnh lớn nhất, thì ta có câu hay và khó là: Chứng minh MN > BC.