Học tốt Toán 7, Phần hình học, Ôn tập chương II
Giải Sách
2019-08-31T11:19:38-04:00
2019-08-31T11:19:38-04:00
https://baihochay.com/index.php/toan-hoc-7/hoc-tot-toan-7-phan-hinh-hoc-on-tap-chuong-ii-3769.html
/themes/linebox/images/no_image.gif
Bài học hay
https://baihochay.com/uploads/bai-hoc-hay-logo.png
Thứ bảy - 31/08/2019 11:19
Hệ thống kiến thức lí thuyết cần nhớ, hướng dẫn giải bài tập SGK Toán 7, Ôn tập chương II
A. Ví dụ giải toánVí dụ. Cho ∆ ABC. Gọi M là trung điếm cạnh BC. Trên tia đối của tia MA lấy điếm D sao cho MD = MA. Từ D vẽ tia Dx vuông góc với BC tại E, trên tia Dx lấy điểm K sao cho E là trung điếm của DK. Chứng minh rằng:a) AC // BD.b) MA = MK.c) AK//BC.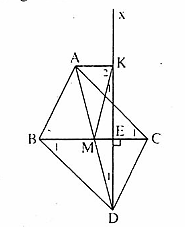 Giải. a) ∆ AMC và ∆ DMB có:BM - MC (giả thiết); MA = MD (giả thiết); AMC = BMD (đối đỉnh).Do đó ∆ AMC = ∆ DMB (c.g.c) nên
Giải. a) ∆ AMC và ∆ DMB có:BM - MC (giả thiết); MA = MD (giả thiết); AMC = BMD (đối đỉnh).Do đó ∆ AMC = ∆ DMB (c.g.c) nên 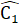 =
= 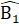 , mà hai góc ớ vị trí so le trong suy ra AC // BD.b) ∆ MKE và ∆ MDEcó:
, mà hai góc ớ vị trí so le trong suy ra AC // BD.b) ∆ MKE và ∆ MDEcó: 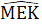 =
= 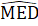 = 90°; KE = ED (giá thiết); ME là cạnh chung.Do đó ∆ MKE = A MDE (c.g.c) nên MK = MD.Mặt khác MA = MD nên MA = MK.c) ∆ MDK cân nên
= 90°; KE = ED (giá thiết); ME là cạnh chung.Do đó ∆ MKE = A MDE (c.g.c) nên MK = MD.Mặt khác MA = MD nên MA = MK.c) ∆ MDK cân nên 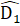 =
= 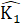 ; ∆ MAK cán nên
; ∆ MAK cán nên 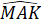 = K2
= K2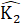 .∆
.∆ AKD có
AKD có 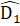 +
+ 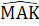 +
+ 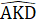 = 180°, hay
= 180°, hay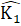 =
= 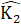 +
+ 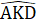 = 180° => 2.
= 180° => 2.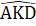 = 180° =>
= 180° => 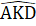 = 90°Suy ra AK ⊥ KD, do đó AK // BC (cùng vuông góc KD).Nhận xét. Qua lời giải của bài toán, chúng ta có thêm cách nhận biết tam giác vuông: Trong một tam giác, đường trung tuyến bằng nứa cạnh đối diện thì tam giác đó là tam giác vuông.B. Hướng dẫn giải bài tập trong sách giáo khoaBài 67. Câu 1 đúng. Càu 2 đúng.Câu 3 sai. Chẳng hạn trong tam giác vuông, góc lớn nhất là góc vuông.Càu 4 sai. Sửa lại cho đúng: Trong một tam giác vuông, hai góc nhọn phụ nhau.Câu 5 đúng.Câu 6 sai. Chẳng hạn có tam giác cân mà góc ở đỉnh bằng 100°.Bài 68. Các câu a, b được suy ra từ định lí "Tổng ba góc của một tam giác bằng 180°".Câu c được suy ra từ định lí "Trong tam giác cân, hai góc ớ đáy bằng nhau".Câu d được suy ra từ định lí "Nếu một tam giác có hai góc băng nhau thì tam giác đó là tam giác cán".Bài 69. (bạn đọc tự vẽ hình)∆ ABD = ∆ ACD(c.c.c) =>
= 90°Suy ra AK ⊥ KD, do đó AK // BC (cùng vuông góc KD).Nhận xét. Qua lời giải của bài toán, chúng ta có thêm cách nhận biết tam giác vuông: Trong một tam giác, đường trung tuyến bằng nứa cạnh đối diện thì tam giác đó là tam giác vuông.B. Hướng dẫn giải bài tập trong sách giáo khoaBài 67. Câu 1 đúng. Càu 2 đúng.Câu 3 sai. Chẳng hạn trong tam giác vuông, góc lớn nhất là góc vuông.Càu 4 sai. Sửa lại cho đúng: Trong một tam giác vuông, hai góc nhọn phụ nhau.Câu 5 đúng.Câu 6 sai. Chẳng hạn có tam giác cân mà góc ở đỉnh bằng 100°.Bài 68. Các câu a, b được suy ra từ định lí "Tổng ba góc của một tam giác bằng 180°".Câu c được suy ra từ định lí "Trong tam giác cân, hai góc ớ đáy bằng nhau".Câu d được suy ra từ định lí "Nếu một tam giác có hai góc băng nhau thì tam giác đó là tam giác cán".Bài 69. (bạn đọc tự vẽ hình)∆ ABD = ∆ ACD(c.c.c) => 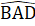 =
= 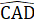 .Gọi H là giao điểm của AD và a. Ta có ∆ AHB = ∆ AHC(c.g.c),từ đó chứng minh được AH ⊥ a, tức là AD ⊥ a.Bài 70. a) ∆ ABC cân =>
.Gọi H là giao điểm của AD và a. Ta có ∆ AHB = ∆ AHC(c.g.c),từ đó chứng minh được AH ⊥ a, tức là AD ⊥ a.Bài 70. a) ∆ ABC cân => 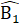 =
= 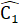 , =>
, => 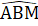 =
= 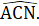 ∆ ABM = ∆ CAN (c.g.c) suy ra
∆ ABM = ∆ CAN (c.g.c) suy ra 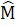 =
= 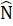 => ∆ ABN là tam giác cânb) ∆ BHM = ∆ CKN (cạnh huyền – góc nhọn) => BH = CK
=> ∆ ABN là tam giác cânb) ∆ BHM = ∆ CKN (cạnh huyền – góc nhọn) => BH = CK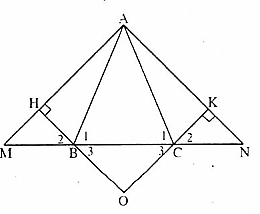 c) ∆ ABH = ∆ ACH ( cạnh huyền – cạnh góc vuông)=> AH = AKd) ∆ BHM = ∆ CKN (câu b), suy ra:
c) ∆ ABH = ∆ ACH ( cạnh huyền – cạnh góc vuông)=> AH = AKd) ∆ BHM = ∆ CKN (câu b), suy ra: 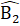 =
= 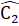 =>
=> 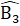 =
= 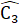 => ∆ OBC là tam giác cân.e) ∆ ABC cân có
=> ∆ OBC là tam giác cân.e) ∆ ABC cân có 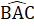 = 60°nên là tam giác đều suy ra
= 60°nên là tam giác đều suy ra 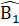 =
= 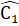 = 60° .
= 60° .
∆ABM có AB = BM (cùng bằng BC) nên là tam giác cân,do 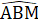 = 120° nên M =
= 120° nên M = 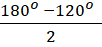 = 30°.Tương tự
= 30°.Tương tự 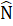 = 30°.∆ AMN có
= 30°.∆ AMN có 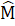 =
= 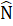 = 30° ,
= 30° , 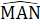 = 120°.∆ MHB vuông có
= 120°.∆ MHB vuông có 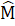 = 30° nên
= 30° nên 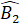 = 60°, suy ra
= 60°, suy ra 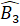 = 60°, ∆ OBC cân (câu d) có
= 60°, ∆ OBC cân (câu d) có 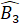 = 60°, nên là tam giác đềuVậy ∆ ABC là tam giác vuông cân.71. ∆ AHB = ∆
= 60°, nên là tam giác đềuVậy ∆ ABC là tam giác vuông cân.71. ∆ AHB = ∆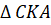 (c.g.c) => AB = CA,
(c.g.c) => AB = CA, 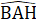 =
= 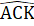 .Ta lại có:
.Ta lại có: 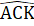 +
+ 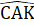 = 90o nên
= 90o nên 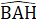 +
+ 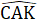 = 90oVậy ∆ ABC là tam giác vuông cân.
= 90oVậy ∆ ABC là tam giác vuông cân.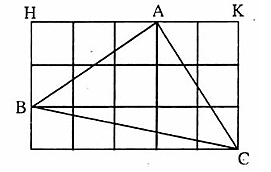 Bài 72. Xem hình vẽ.
Bài 72. Xem hình vẽ.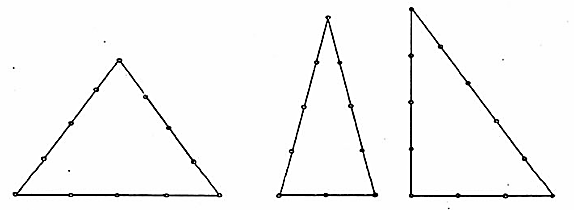 73. ∆ AHB vuông tại H nên:HB2 = AB2 - AH2 = 52 -32 = 16; HB = 4m; HC = 10 - 4 = 6 (m).∆ AHC vuông tại H nên: AC2 = AH2 + HC2 = 32 + 62 = 45 .Suy ra AC =
73. ∆ AHB vuông tại H nên:HB2 = AB2 - AH2 = 52 -32 = 16; HB = 4m; HC = 10 - 4 = 6 (m).∆ AHC vuông tại H nên: AC2 = AH2 + HC2 = 32 + 62 = 45 .Suy ra AC = 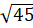 ≈ 6,7(m).Độ dài đường trượt ACD bằng: 6,7 + 2 = 8,7 (m), chưa bằng hai lần đường lên BA.Vậy Vân đúng, Mai sai.C. Bài tập luyện thêmCho ∆ ABC có AB < AC và tia phân giác AD (D ∈ BC). Trên AC lấy E sao cho AE = AB. Trên tia AB lấy điểm F sao cho AF = AC.a) Chứng minh: DB = DE, BF = CE.b) Chứng minh: F, D, E thẳng hàng.c) Chứng minh: BE // FC và AD ⊥ FC.d) Chứng minh góc ADC là góc tù.2. Cho ∆ ABC cân tại A. Gọi M là trung điểm của cạnh BC. Gọi I là trung điểm đoạn thẳng AM. Trên tia CI lấy điểm N sao cho CN = 2.CI.a) Chứng minh AN // BC.b) Trên tia BI lấy điểm K sao cho BK = 2.BI. Chứng minh A là trung điểm của NK.3. Cho ∆ ABC có A = 90° ; B = 50° . Tia phân giác của góc B cắt AC ở D.a) Tính số đo góc BDC ?b) Lấy điểm H trên tia BC sao cho BH = BA.Chứng minh ∆ BDH = ∆ BDA.c) Lấy điểm E trên tia BH sao cho
≈ 6,7(m).Độ dài đường trượt ACD bằng: 6,7 + 2 = 8,7 (m), chưa bằng hai lần đường lên BA.Vậy Vân đúng, Mai sai.C. Bài tập luyện thêmCho ∆ ABC có AB < AC và tia phân giác AD (D ∈ BC). Trên AC lấy E sao cho AE = AB. Trên tia AB lấy điểm F sao cho AF = AC.a) Chứng minh: DB = DE, BF = CE.b) Chứng minh: F, D, E thẳng hàng.c) Chứng minh: BE // FC và AD ⊥ FC.d) Chứng minh góc ADC là góc tù.2. Cho ∆ ABC cân tại A. Gọi M là trung điểm của cạnh BC. Gọi I là trung điểm đoạn thẳng AM. Trên tia CI lấy điểm N sao cho CN = 2.CI.a) Chứng minh AN // BC.b) Trên tia BI lấy điểm K sao cho BK = 2.BI. Chứng minh A là trung điểm của NK.3. Cho ∆ ABC có A = 90° ; B = 50° . Tia phân giác của góc B cắt AC ở D.a) Tính số đo góc BDC ?b) Lấy điểm H trên tia BC sao cho BH = BA.Chứng minh ∆ BDH = ∆ BDA.c) Lấy điểm E trên tia BH sao cho 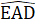 = 50°.Chứng minh: AE // DH.4. Cho ∆ ABC có BC = 2.AB. Gọi M là trung điểm của BC và D là trung điểm của BM. Chứng minh AC = 2.AD.Lời giải - Hướng dẫn - Đáp sốa) Xét ∆ ABD và ∆ AED có:AB = AE (giả thiết);Â1 = Â2 (giả thiết);AD là cạnh chung.Do đó ∆ ABD = ∆ AED (c.g.g) nên BD = ED.Ta có AF = AC, AB = AE => BF = CE.
= 50°.Chứng minh: AE // DH.4. Cho ∆ ABC có BC = 2.AB. Gọi M là trung điểm của BC và D là trung điểm của BM. Chứng minh AC = 2.AD.Lời giải - Hướng dẫn - Đáp sốa) Xét ∆ ABD và ∆ AED có:AB = AE (giả thiết);Â1 = Â2 (giả thiết);AD là cạnh chung.Do đó ∆ ABD = ∆ AED (c.g.g) nên BD = ED.Ta có AF = AC, AB = AE => BF = CE.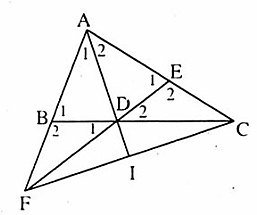 b) ∆ ABD = ∆ AED (chứng minh trên) nên
b) ∆ ABD = ∆ AED (chứng minh trên) nên 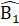 =
= 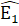 =>
=> 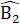 =
= 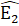 .Xét ∆ BDF và ∆ EDC có: BD = ED; ; BF = EC.Do đó ∆ BDF = ∆ EDC (c.g.c) nên
.Xét ∆ BDF và ∆ EDC có: BD = ED; ; BF = EC.Do đó ∆ BDF = ∆ EDC (c.g.c) nên 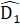 =
= 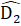 . .Mặt khác
. .Mặt khác 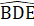 +
+ 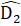 . = 180°, suy ra
. = 180°, suy ra 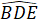 +
+ 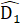 , =180° hay F, D, E thẳng hàng.c) Gọi giao điểm của đường thẳng AD và CF là I.Xét ∆ AFI và ∆ ACI có: AF = AC; Â1 = Â2 ; AI chung,do đó ∆ AIF = ∆ AIC (c.g.c) nên
, =180° hay F, D, E thẳng hàng.c) Gọi giao điểm của đường thẳng AD và CF là I.Xét ∆ AFI và ∆ ACI có: AF = AC; Â1 = Â2 ; AI chung,do đó ∆ AIF = ∆ AIC (c.g.c) nên 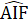 =
= 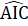 , mà
, mà 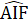 +
+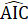 = 180°suy ra
= 180°suy ra 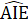 =
= 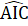 = 90° => AI ⊥ CF .Chứng minh tưomg tự AD ⊥ BE, do đó BE// FC.d) AB = AE, AB < AC nên AE < AC => E nằm giữa A và C.Suy ra
= 90° => AI ⊥ CF .Chứng minh tưomg tự AD ⊥ BE, do đó BE// FC.d) AB = AE, AB < AC nên AE < AC => E nằm giữa A và C.Suy ra 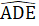 <
< 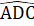 mặc khác
mặc khác 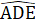 =
= 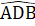 =>
=> 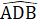 <
< 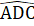 Mà
Mà 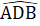 +
+ 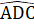 = 180o =>
= 180o => 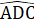 > 90°.2. a) Xét ∆ AIN và ∆ MIC có:AI = IM (giả thiết);
> 90°.2. a) Xét ∆ AIN và ∆ MIC có:AI = IM (giả thiết);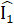 =
= 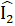 . (đối đỉnh);IC = IN (giả thiết).Do đó ∆ AIN = ∆ MIC (c.g.c), do đó
. (đối đỉnh);IC = IN (giả thiết).Do đó ∆ AIN = ∆ MIC (c.g.c), do đó 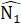 =
= 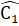 , mà hai góc ở vị trí so le trong, vậy AN // BC.
, mà hai góc ở vị trí so le trong, vậy AN // BC.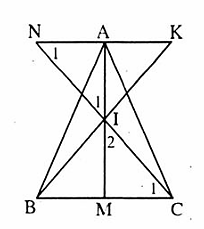 b) Chứng minh tương tự ∆ AIK = ∆ MIB (c.g.c)=> AK = BM và AK // BC. Mà AN // BC nên N, A, K thẳng hàng.Mặt khác AN = MC (vì ∆ AIN = ∆ MIC), AK = BM và MC = BM (giả thiết)nên suy ra AN = AK. Vậy A là trung điểm của NK.3. a) ∆ ABC có Â = 90o;
b) Chứng minh tương tự ∆ AIK = ∆ MIB (c.g.c)=> AK = BM và AK // BC. Mà AN // BC nên N, A, K thẳng hàng.Mặt khác AN = MC (vì ∆ AIN = ∆ MIC), AK = BM và MC = BM (giả thiết)nên suy ra AN = AK. Vậy A là trung điểm của NK.3. a) ∆ ABC có Â = 90o; 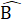 =50o nên
=50o nên 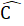 = 40o
= 40o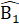 =
= 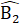 =
= 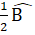 = 25o (vì BD là tia phân giác của góc B)Xét ∆ BDC có
= 25o (vì BD là tia phân giác của góc B)Xét ∆ BDC có 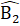 =
= 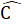 +
+ 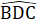 = 180o=> 25o + 40o +
= 180o=> 25o + 40o + 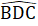 = 180o => 115o.b) ∆ BAD = ∆ BHD (c.g.c).c) ∆ BAD = ∆ BHD nên
= 180o => 115o.b) ∆ BAD = ∆ BHD (c.g.c).c) ∆ BAD = ∆ BHD nên 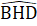 =
= 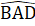 =>
=> 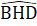 = 90o => BC ⊥ DH.Xét ∆ ACE có
= 90o => BC ⊥ DH.Xét ∆ ACE có 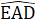 +
+ 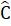 = 50o + 40o = 90o nên ∆ ACE vuông tại E => AE ⊥ BC. Suy ra DH // AE (vì cùng vuông góc BC).
= 50o + 40o = 90o nên ∆ ACE vuông tại E => AE ⊥ BC. Suy ra DH // AE (vì cùng vuông góc BC).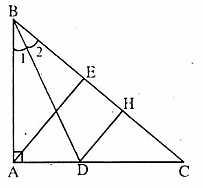 4. Trên tia đối của tia DA lấy điểm E sao cho DE = DA.Dễ có ∆ADB = ∆EDM (c.g.c) nên AB = ME.
4. Trên tia đối của tia DA lấy điểm E sao cho DE = DA.Dễ có ∆ADB = ∆EDM (c.g.c) nên AB = ME. 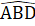 =
= 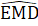 .Suy ra ME = AB = MC =
.Suy ra ME = AB = MC =  BC.
BC.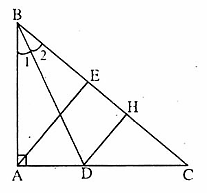 Mặt khác
Mặt khác 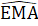 =
= 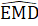 +
+ 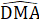
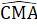 =
= 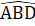 +
+ 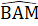 (góc ngoài tam giác)
(góc ngoài tam giác)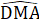 =
= 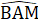 (∆ ABM cân)Từ đó suy ra
(∆ ABM cân)Từ đó suy ra 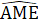 =
= 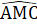 .Do đó ∆AME = ∆AMC (c.g.c) => AC = AE = 2.AD.
.Do đó ∆AME = ∆AMC (c.g.c) => AC = AE = 2.AD.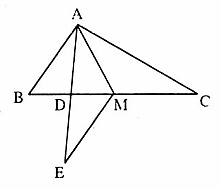 Nhận xét. Về mặt phương pháp rất tự nhiên, muốn chứng minh đoạn thẳng AC = 2.AD, ta cần tạo ra một đoạn thẳng bằng 2.AD sau đó chứng minh hai đoạn thẳng bằng nhau.
Nhận xét. Về mặt phương pháp rất tự nhiên, muốn chứng minh đoạn thẳng AC = 2.AD, ta cần tạo ra một đoạn thẳng bằng 2.AD sau đó chứng minh hai đoạn thẳng bằng nhau.